ГДЗ по Алгебре 7 Класс Номер 518 Дорофеев, Суворова — Подробные Ответы

Прямоугольник задан усло- виями
\(1 \leq x \leq 3\) и \(1 \leq y \leq 2\).

Изобразите на координат- ной плоскости и опишите на алгебраическом языке множество точек, симмет- ричных этому прямо- угольнику относительно:
а) оси ординат;
б) оси абсцисс;
в) начала координат.

Дан прямоугольник: \(1 \le x \le 3,\; 1 \le y \le 2\).

а) При симметрии относительно оси ординат каждая точка \((x,y)\) переходит в \((-x,y)\), значит \(x\) меняет знак, а \(y\) остаётся тем же. Интервал \(1 \le x \le 3\) переходит в \(-3 \le x \le -1\), \(y\) не меняется: \(-3 \le x \le -1,\; 1 \le y \le 2\).

б) При симметрии относительно оси абсцисс точка \((x,y)\) переходит в \((x,-y)\), значит \(y\) меняет знак, а \(x\) остаётся тем же. Интервал \(1 \le y \le 2\) переходит в \(-2 \le y \le -1\), \(x\) не меняется: \(1 \le x \le 3,\; -2 \le y \le -1\).

в) При симметрии относительно начала координат точка \((x,y)\) переходит в \((-x,-y)\), меняются знаки и у \(x\), и у \(y\). Тогда получаем: \(-3 \le x \le -1,\; -2 \le y \le -1\).

Дан исходный прямоугольник, заданный системой неравенств: \(1 \le x \le 3,\; 1 \le y \le 2\). Это значит, что рассматривается множество всех точек \((x,y)\) на координатной плоскости, у которых абсцисса \(x\) лежит между 1 и 3 включительно, а ордината \(y\) лежит между 1 и 2 включительно. Геометрически это прямоугольник в первой четверти, его вершины имеют координаты \((1,1),\ (3,1),\ (3,2),\ (1,2)\). При симметриях относительно осей и начала координат меняются знаки координат точек, а сами длины отрезков, то есть размеры прямоугольника по горизонтали и вертикали, сохраняются. Поэтому во всех трёх случаях у нас будут прямоугольники такой же «величины», но расположенные в других четвертях координатной плоскости.

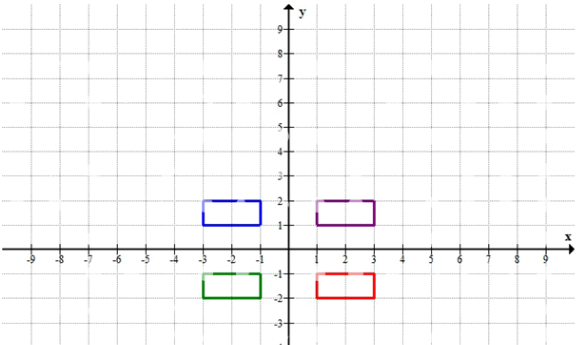
а) Симметрия относительно оси ординат означает, что мы отражаем каждую точку относительно вертикальной оси \(Oy\). При таком отражении абсцисса \(x\) меняет знак, а ордината \(y\) остаётся неизменной: точка \((x,y)\) переходит в точку \((-x,y)\). Поэтому для исходного диапазона \(1 \le x \le 3\) после отражения получаем диапазон для новой координаты \(-x\): числа от 1 до 3 по модулю «переезжают» на левую сторону, то есть интервал становится \(-3 \le x \le -1\). При этом ордината \(y\) не меняется, так как отражение относительно оси ординат не «поднимает» и не «опускает» точки, а лишь переносит их влево или вправо. Следовательно, условие для \(y\) остаётся тем же: \(1 \le y \le 2\). Таким образом, прямоугольник, симметричный исходному относительно оси ординат (синий на рисунке), задаётся неравенствами: \(-3 \le x \le -1,\; 1 \le y \le 2\).

б) Симметрия относительно оси абсцисс означает отражение относительно горизонтальной оси \(Ox\). В этом случае, наоборот, абсцисса \(x\) остаётся той же, а ордината \(y\) меняет знак: точка \((x,y)\) переходит в точку \((x,-y)\). Исходный интервал для \(x\), то есть \(1 \le x \le 3\), не меняется, потому что отражение идёт «вверх-вниз», а не «влево-вправо». Зато интервал для \(y\) меняется: значения \(y\) из промежутка от 1 до 2 при изменении знака переходят в значения от \(-1\) до \(-2\), но так как мы всегда записываем интервалы слева направо от меньшего числа к большему, получаем диапазон \(-2 \le y \le -1\). Значит, прямоугольник, симметричный исходному относительно оси абсцисс (красный на рисунке), описывается условиями: \(1 \le x \le 3,\; -2 \le y \le -1\).

в) Симметрия относительно начала координат можно рассматривать как последовательное отражение сначала относительно одной оси, а затем относительно другой, либо как одновременное изменение знаков обеих координат. При такой симметрии каждая точка \((x,y)\) переходит в точку \((-x,-y)\). Поэтому для абсциссы \(x\), которая в исходном прямоугольнике удовлетворяет неравенству \(1 \le x \le 3\), новое значение \(-x\) будет находиться в промежутке от \(-3\) до \(-1\), то есть получаем \(-3 \le x \le -1\). Аналогично, исходный интервал для ординаты \(y\), равный \(1 \le y \le 2\), при смене знака превращается в интервал \(-2 \le y \le -1\). В итоге прямоугольник, симметричный исходному относительно начала координат (зелёный на рисунке), задаётся системой неравенств: \(-3 \le x \le -1,\; -2 \le y \le -1\).