ГДЗ по Алгебре 7 Класс Номер 517 Дорофеев, Суворова — Подробные Ответы

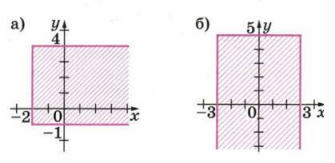
Задайте с помощью неравенств множества точек координатной плоскости, изображённые на рисунке 5.49, a, б.

a) \(x \ge -2\), \(-1 \le y \le 4\).

Это множество всех точек плоскости, у которых абсцисса не меньше \(-2\), а ордината изменяется от \(-1\) до \(4\) включительно.

б) \(y \le 5\), \(-3 \le x \le 3\).

Это множество всех точек плоскости, у которых ордината не больше \(5\), а абсцисса изменяется от \(-3\) до \(3\) включительно.

a) Неравенство \(x \ge -2\) задаёт все точки плоскости, которые находятся на вертикальной прямой \(x = -2\) и правее неё. Это значит, что любая точка с координатами \((x; y)\), у которой первая координата не меньше \(-2\), принадлежит данному множеству. Неравенство \(-1 \le y \le 4\) задаёт полосу между двумя горизонтальными прямыми \(y = -1\) и \(y = 4\), включая эти границы. То есть вторая координата точки может принимать значения от \(-1\) до \(4\) включительно.

Если объединить оба условия, то получим пересечение вертикальной полуплоскости \(x \ge -2\) и горизонтальной полосы \(-1 \le y \le 4\). Геометрически это прямоугольная полоса, «обрезанная» слева вертикальной прямой \(x = -2\). Все точки внутри этой области, а также точки на границах \(x = -2\), \(y = -1\) и \(y = 4\), удовлетворяют системе неравенств. Поэтому множество точек для части а) описывается системой: \(x \ge -2\), \(-1 \le y \le 4\).

б) Неравенство \(y \le 5\) задаёт множество всех точек, расположенных на горизонтальной прямой \(y = 5\) и ниже неё. То есть вторая координата \(y\) может быть любой, но не больше \(5\). Неравенство \(-3 \le x \le 3\) задаёт вертикальную полосу между прямыми \(x = -3\) и \(x = 3\), причём обе граничные прямые включены в множество, так как неравенства нестрогие.

Совместное выполнение этих двух неравенств даёт пересечение вертикальной полосы \(-3 \le x \le 3\) и нижней полуплоскости \(y \le 5\). В результате получается полосообразная область шириной от \(-3\) до \(3\) по оси \(x\), ограниченная сверху прямой \(y = 5\) и неограниченная вниз. Все точки внутри этой области и на её границах \(x = -3\), \(x = 3\) и \(y = 5\) принадлежат искомому множеству. Поэтому множество точек для части б) задаётся системой: \(y \le 5\), \(-3 \le x \le 3\).