ГДЗ по Алгебре 7 Класс Номер 516 Дорофеев, Суворова — Подробные Ответы

Постройте ломаную \(ABCD\) по описанию её звеньев:
a) \(AB: x=-5\) и \(|y|\le5;\)
\(BC: y=x\) и \(|x|\le5;\)
\(CD: y=5\) и \(0\le x\le5;\)

б) \(AB: x=-3\) и \(-3\le y\le3;\)
\(BC: y=x\) и \(-3\le x\le5;\)
\(CD: x=5\) и \(-5\le y\le5.\)

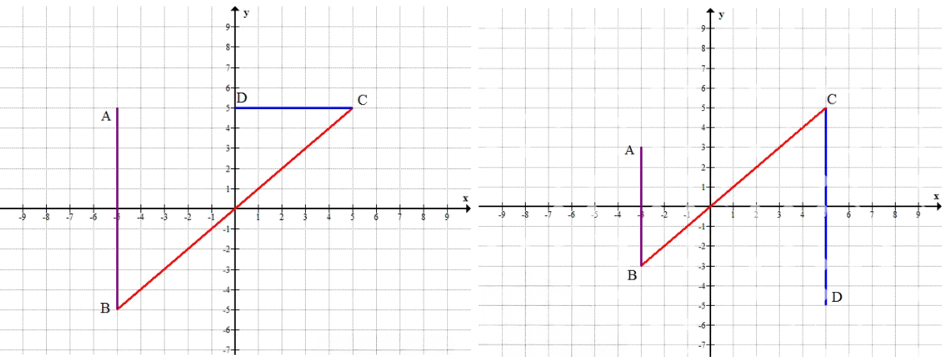
a) На отрезке \(AB\) берём все точки с координатами \(x=-5\) и \(|y|\le5\): вертикальный отрезок на прямой \(x=-5\) от \(y=-5\) до \(y=5\).

На отрезке \(BC\) берём все точки прямой \(y=x\) при \(|x|\le5\): диагональный отрезок от \((-5,-5)\) до \((5,5)\).

На отрезке \(CD\) берём точки с \(y=5\) и \(0\le x\le5\): горизонтальный отрезок от \((0,5)\) до \((5,5)\).

б) На отрезке \(AB\) точки имеют координаты \(x=-3\) и \(-3\le y\le3\): вертикальный отрезок на прямой \(x=-3\) от \(y=-3\) до \(y=3\).

На отрезке \(BC\) точки прямой \(y=x\) при \(-3\le x\le5\): диагональный отрезок от \((-3,-3)\) до \((5,5)\).

На отрезке \(CD\) точки с \(x=5\) и \(-5\le y\le5\): вертикальный отрезок на прямой \(x=5\) от \(y=-5\) до \(y=5\).

a) Для построения звена \(AB\) по условию \(x=-5\) и \(|y|\le5\) сначала понимаем, что у всех точек этого отрезка абсцисса одна и та же: \(x=-5\). Это означает, что все точки лежат на вертикальной прямой, проходящей через \(-5\) по оси \(x\). Неравенство \(|y|\le5\) означает, что ордината \(y\) может принимать все значения от \(-5\) до \(5\), включая границы. Значит, мы отмечаем на прямой \(x=-5\) точки с координатами \((-5,-5)\) и \((-5,5)\), а затем соединяем их отрезком. Верхнюю точку \((-5,5)\) обозначаем буквой \(A\), нижнюю \((-5,-5)\) буквой \(B\), поскольку по рисунку ломаная идёт по порядку \(A \rightarrow B \rightarrow C \rightarrow D\) или наоборот, но сами координаты этих точек однозначно определяются описанием.

Далее строим звено \(BC\) по описанию \(y=x\) и \(|x|\le5\). Условие \(y=x\) задаёт прямую, проходящую через начало координат и все точки, где абсцисса равна ординате, например \((-3,-3)\), \((0,0)\), \((4,4)\) и т. д. Условие \(|x|\le5\) означает, что \(x\) изменяется от \(-5\) до \(5\), включая эти значения. Соответственно, отрезок \(BC\) будет частью диагонали от точки \((-5,-5)\), которая совпадает с точкой \(B\), до точки \((5,5)\). Именно эта точка \((5,5)\) будет концом звена \(BC\) и в ломаной обозначается буквой \(C\). Таким образом, \(BC\) – наклонный отрезок по прямой \(y=x\), связывающий \(B(-5,-5)\) и \(C(5,5)\).

Наконец, строим звено \(CD\) по описанию \(y=5\) и \(0\le x\le5\). Условие \(y=5\) задаёт горизонтальную прямую, параллельную оси \(x\), проходящую через точку \((0,5)\). Ограничение \(0\le x\le5\) означает, что берем часть этой прямой между точками с абсциссами \(0\) и \(5\), то есть от \((0,5)\) до \((5,5)\). Точка \((5,5)\) уже получена как вершина \(C\), поэтому ломаная продолжится от \(C(5,5)\) до \(D(0,5)\). В вершине при \(x=0\), \(y=5\) ставим букву \(D\). В итоге для пункта a) ломаная \(ABCD\) состоит из вертикального отрезка \(AB\) на прямой \(x=-5\), наклонного отрезка \(BC\) на прямой \(y=x\) и горизонтального отрезка \(CD\) на прямой \(y=5\), причём вершины имеют координаты \(A(-5,5)\), \(B(-5,-5)\), \(C(5,5)\), \(D(0,5)\).

б) В пункте б) сначала строим звено \(AB\) по условию \(x=-3\) и \(-3\le y\le3\). Здесь, как и в пункте a), фиксированная абсцисса \(x=-3\) задаёт вертикальную прямую, расположенную левее оси \(y\). Неравенство \(-3\le y\le3\) говорит, что берём участок этой прямой от точки \((-3,-3)\) до точки \((-3,3)\) включительно. Эти две крайние точки являются концами отрезка \(AB\); одну из них (обычно верхнюю) обозначаем как \(A(-3,3)\), другую как \(B(-3,-3)\). Таким образом, \(AB\) – вертикальный отрезок высотой \(6\) единиц, строго ограниченный по оси \(y\) от \(-3\) до \(3\).

Затем рассматриваем звено \(BC\), заданное уравнением \(y=x\) и неравенством \(-3\le x\le5\). Уравнение \(y=x\) снова задаёт диагональ, как и в пункте a), но теперь мы берём только её часть, где \(x\) изменяется от \(-3\) до \(5\). При \(x=-3\) получаем точку \((-3,-3)\), которая как раз совпадает с точкой \(B\), уже построенной на отрезке \(AB\). При \(x=5\) имеем точку \((5,5)\), которая станет новой вершиной \(C\). Соединяя точки \((-3,-3)\) и \((5,5)\) по прямой \(y=x\), получаем наклонный отрезок \(BC\). По рисунку он идёт из левой нижней части к правой верхней, проходя через начало координат \((0,0)\), поскольку при \(x=0\) также имеем \(y=0\).

Последнее звено \(CD\) описано условиями \(x=5\) и \(-5\le y\le5\). Здесь фиксированная абсцисса \(x=5\) задаёт вертикальную прямую, симметричную относительно оси \(y\) к прямой \(x=-5\) из пункта a). Неравенство по \(y\) означает, что берём участок этой прямой от точки \((5,-5)\) до \((5,5)\), включая обе границы. Точка \((5,5)\) уже является вершиной \(C\), поэтому мы продолжаем ломаную вниз по прямой \(x=5\) до точки \((5,-5)\), которую обозначаем буквой \(D\). В результате ломаная \(ABCD\) в пункте б) состоит из вертикального отрезка \(AB\) на прямой \(x=-3\), наклонного отрезка \(BC\) по прямой \(y=x\) от \((-3,-3)\) до \((5,5)\) и вертикального отрезка \(CD\) на прямой \(x=5\) от \((5,5)\) до \((5,-5)\); координаты вершин: \(A(-3,3)\), \(B(-3,-3)\), \(C(5,5)\), \(D(5,-5)\).