ГДЗ по Алгебре 7 Класс Номер 515 Дорофеев, Суворова — Подробные Ответы

Прочитайте неравенство, используя слово «расстояние», и найдите с помощью координатной прямой множество точек, координаты которых удовлетворяют этому неравенству:

а) \(|x| > |x — 1|\);

б) \(|x + 2| < |x — 2|\).

а) \(|x| \geq |x — 1|\)
Расстояние от точки \(x\) до точки 0 больше или равно расстоянию от точки \(x\) до точки 1. Найдём середину отрезка с концами в точках 0 и 1:
\( \frac{0 + 1}{2} = 0,5 \).
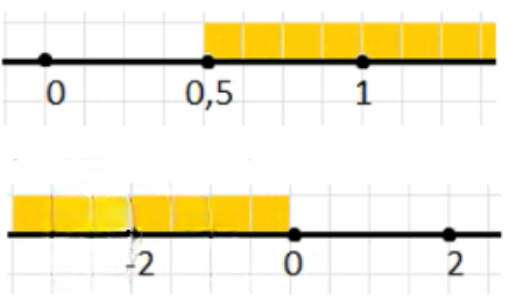
Следовательно, \(x \geq 0,5\).

б) \(|x + 2| \leq |x — 2|\)
Расстояние от точки \(x\) до точки \(-2\) меньше или равно расстоянию от точки \(x\) до точки 2. Найдём середину отрезка с концами в точках \(-2\) и 2:
\(\frac{-2 + 2}{2} = 0\).
Следовательно, \(x \leq 0\).

а) Рассмотрим неравенство \(|x| \geq |x — 1|\). По определению модуля абсолютное значение числа \(x\) — это расстояние от точки с координатой \(x\) до точки 0 на числовой оси. Аналогично, \(|x — 1|\) — это расстояние от точки \(x\) до точки 1. Неравенство говорит, что расстояние от точки \(x\) до 0 больше или равно расстоянию от точки \(x\) до 1.

Чтобы понять, при каких значениях \(x\) это возможно, найдем точку, которая находится ровно посередине между 0 и 1. Середина отрезка с концами в точках 0 и 1 находится по формуле среднего арифметического: \( \frac{0 + 1}{2} = 0,5 \). Эта точка делит отрезок на две равные части.

Если точка \(x\) расположена правее этой середины, то расстояние до 0 будет больше, чем до 1, что удовлетворяет неравенству. Если же \(x\) левее 0,5, расстояние до 1 будет меньше, и неравенство не выполняется. Следовательно, множество решений — все \(x\), для которых \(x \geq 0,5\).

б) Рассмотрим неравенство \(|x + 2| \leq |x — 2|\). Модуль \(|x + 2|\) — это расстояние от точки \(x\) до точки \(-2\), а \(|x — 2|\) — расстояние от точки \(x\) до точки 2. Неравенство означает, что расстояние от \(x\) до \(-2\) меньше или равно расстоянию от \(x\) до 2.

Для анализа найдем середину отрезка с концами в точках \(-2\) и 2. Середина вычисляется как \( \frac{-2 + 2}{2} = 0 \). Эта точка разделяет числовую ось на две части, и на каждой из них расстояния до концов отрезка ведут себя по-разному.

Если \(x\) находится слева от 0, то точка ближе к \(-2\), и расстояние до \(-2\) меньше или равно расстоянию до 2, что удовлетворяет неравенству. Если \(x\) правее 0, то расстояние до 2 меньше, и неравенство не выполняется. Следовательно, решение — все \(x\), для которых \(x \leq 0\).