ГДЗ по Алгебре 7 Класс Номер 512 Дорофеев, Суворова — Подробные Ответы

Изобразите на координатной прямой множество точек, координаты которых удовлетворяют уравнению или неравенству:

а) \(|x-4|=2\), \(|x-4|<2\), \(|x-4|>2\);

б) \(|x+3|=4\), \(|x+3|<4\), \(|x+3|>4\).

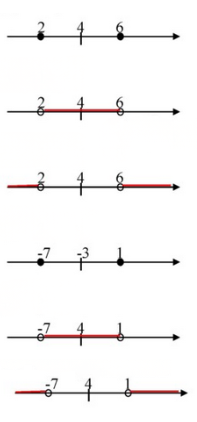
а) \(|x-4|=2\)
Решаем уравнение:
\(x-4=2 \Rightarrow x=6\),
\(x-4=-2 \Rightarrow x=2\).
Корни: \(x=2, 6\).

\(|x-4|<2\)
Раскрываем неравенство:
\(x\) лежит между 2 и 6, то есть \(2 < x < 6\).

\(|x-4|>2\)
Тогда \(x < 2\) или \(x > 6\).

б) \(|x+3|=4\)
Решаем уравнение:
\(x+3=4 \Rightarrow x=1\),
\(x+3=-4 \Rightarrow x=-7\).
Корни: \(x=-7, 1\).

\(|x+3|<4\)
Тогда \(x\) лежит между \(-7\) и \(1\), то есть \(-7 < x < 1\).

\(|x+3|>4\)
Тогда \(x < -7\) или \(x > 1\).

а) Рассмотрим уравнение \(|x-4|=2\). Модуль выражения \(|x-4|\) равен расстоянию точки \(x\) от числа 4 на числовой оси. Значит, чтобы модуль был равен 2, точка \(x\) должна находиться на расстоянии ровно 2 единицы от 4. Это может быть либо справа, либо слева от 4. Таким образом, уравнение распадается на два линейных уравнения: \(x-4=2\) и \(x-4=-2\). Решая первое, получаем \(x=6\), а второе даёт \(x=2\). Следовательно, решения — это две точки: 2 и 6.

Теперь рассмотрим неравенство \(|x-4|<2\). Это означает, что расстояние от точки \(x\) до числа 4 строго меньше 2. То есть \(x\) находится внутри интервала между точками, которые лежат на расстоянии 2 от 4. Эти точки — 2 и 6, поэтому множество решений — это все \(x\), для которых \(2 < x < 6\). Этот интервал включает все точки между 2 и 6, но не включает сами границы, так как знак неравенства строгий.

Для неравенства \(|x-4|>2\) ситуация обратная: расстояние от \(x\) до 4 должно быть строго больше 2. Значит, \(x\) лежит вне интервала между 2 и 6, то есть либо меньше 2, либо больше 6. Таким образом, множество решений — два интервала: \(x < 2\) и \(x > 6\).

б) Аналогично рассмотрим уравнение \(|x+3|=4\). Модуль \(|x+3|\) — это расстояние точки \(x\) от числа \(-3\). Чтобы оно было равно 4, точка \(x\) должна находиться на расстоянии 4 от \(-3\). Это даёт два уравнения: \(x+3=4\) и \(x+3=-4\). Решая, получаем \(x=1\) и \(x=-7\). Значит, решения — точки \(-7\) и \(1\).

Для неравенства \(|x+3|<4\) точка \(x\) должна находиться на расстоянии меньше 4 от \(-3\). Это значит, что \(x\) лежит внутри интервала между \(-7\) и \(1\), то есть \(-7 < x < 1\). Все точки внутри этого интервала удовлетворяют неравенству.

Если же \(|x+3|>4\), то \(x\) находится вне интервала от \(-7\) до \(1\), то есть либо \(x < -7\), либо \(x > 1\). Это множество решений состоит из двух отдельных интервалов, расположенных по обе стороны от интервала \((-7, 1)\).