ГДЗ по Алгебре 7 Класс Номер 511 Дорофеев, Суворова — Подробные Ответы

Изобразите на плоскости множество точек, координаты которых удовлетворяют равенству:

а) \( y = |x| — x \);

б) \( y = |x| \cdot x \);

в) \( y = \frac{|x|}{x} \);

г) \( y = \frac{2x}{|x|} \).

а) При \( x \geq 0 \), \( |x| = x \), тогда \( y = x — x = 0 \);

при \( x < 0 \), \( |x| = -x \), тогда \( y = -x — x = -2x \);

\( y = \begin{cases}
0, & x \geq 0 \\
-2x, & x < 0
\end{cases} \)

б) При \( x \geq 0 \), \( |x| = x \), тогда \( y = x \cdot x = x^2 \);

при \( x < 0 \), \( |x| = -x \), тогда \( y = -x \cdot x = -x^2 \);

\( y = \begin{cases}
x^2, & x \geq 0 \\
-x^2, & x < 0
\end{cases} \)

в) При \( x > 0 \), \( |x| = x \), тогда \( y = \frac{x}{x} = 1 \);

при \( x < 0 \), \( |x| = -x \), тогда \( y = \frac{-x}{x} = -1 \);

\( y = \begin{cases}
1, & x > 0 \\
-1, & x < 0
\end{cases} \)

г) При \( x > 0 \), \( |x| = x \), тогда \( y = \frac{2x}{x} = 2 \);

при \( x < 0 \), \( |x| = -x \), тогда \( y = \frac{2x}{-x} = -2 \);

\( y = \begin{cases}
2, & x > 0 \\
-2, & x < 0
\end{cases} \)

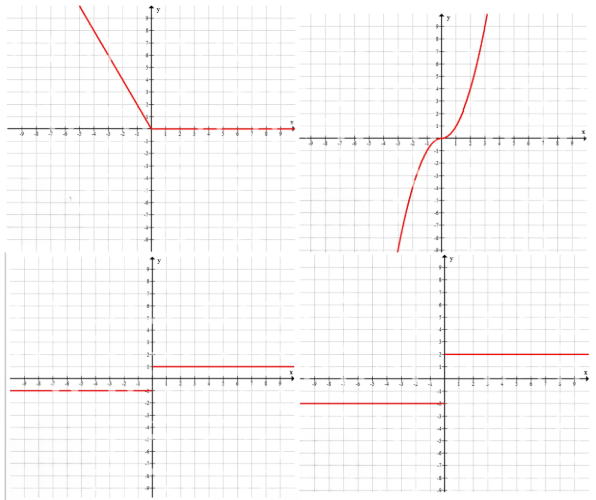
а) Рассмотрим функцию \( y = |x| — x \). Для того чтобы понять, как она ведет себя на плоскости, нужно рассмотреть два случая, так как модуль \( |x| \) зависит от знака \( x \). При \( x \geq 0 \) модуль \( |x| \) равен самому \( x \), то есть \( |x| = x \). Подставляя это в уравнение, получаем \( y = x — x = 0 \). Это означает, что для всех неотрицательных значений \( x \) точка лежит на оси \( x \), то есть \( y = 0 \).

При \( x < 0 \) модуль меняет знак, и \( |x| = -x \). Подставляя это в уравнение, получаем \( y = -x — x = -2x \). Здесь значение \( y \) зависит от \( x \) линейно с коэффициентом \(-2\), но так как \( x \) отрицательно, то \( y \) становится положительным. Таким образом, для отрицательных \( x \) график — это прямая линия с угловым коэффициентом 2, проходящая через начало координат.

Итоговое выражение функции можно записать в виде кусочно-заданной функции:

\( y = 0 \),при \( x \geq 0 \)\( y = -2x \),при \( x < 0 \)

б) Функция \( y = |x| \cdot x \) тоже требует рассмотрения по частям из-за модуля. При \( x \geq 0 \) имеем \( |x| = x \), тогда \( y = x \cdot x = x^2 \). Это классическая парабола, ветви которой направлены вверх, и она касается оси \( x \) в точке \( 0 \).

При \( x < 0 \) модуль меняет знак: \( |x| = -x \), тогда \( y = -x \cdot x = -x^2 \). Здесь получается парабола, направленная вниз, зеркально отраженная относительно оси \( x \) по сравнению с первым случаем.

В итоге функция задается кусочно:

\( y = x^2 \),при \( x \geq 0 \)\( y = -x^2 \),при \( x < 0 \)

в) Рассмотрим функцию \( y = \frac{|x|}{x} \). Здесь важно, что деление на \( x \) запрещено при \( x = 0 \), поэтому \( x \neq 0 \). При \( x > 0 \) модуль равен \( x \), значит \( y = \frac{x}{x} = 1 \). Это значит, что при положительных \( x \) функция постоянна и равна 1.

При \( x < 0 \) модуль равен \( -x \), тогда \( y = \frac{-x}{x} = -1 \). Для отрицательных \( x \) функция также постоянна, но равна \(-1\). Таким образом, график состоит из двух горизонтальных прямых, расположенных на уровнях \( y = 1 \) и \( y = -1 \) соответственно, с разрывом в точке \( x = 0 \).

Функция записывается так:

\( y = 1 \),при \( x > 0 \)\( y = -1 \),при \( x < 0 \)

г) Для функции \( y = \frac{2x}{|x|} \) ситуация аналогична предыдущей. При \( x > 0 \) имеем \( |x| = x \), тогда \( y = \frac{2x}{x} = 2 \). Значит, при положительных \( x \) функция постоянна и равна 2.

При \( x < 0 \) модуль равен \( -x \), тогда \( y = \frac{2x}{-x} = -2 \). Для отрицательных \( x \) функция также постоянна, но равна \(-2\). График состоит из двух горизонтальных линий на уровнях 2 и \(-2\) с разрывом в точке \( x = 0 \).

Функция в виде кусочно-заданной:

\( y = 2 \),при \( x > 0 \)\( y = -2 \),при \( x < 0 \)