ГДЗ по Алгебре 7 Класс Номер 482 Дорофеев, Суворова — Подробные Ответы

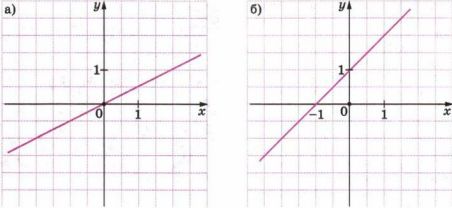
а) Составьте таблицу соответственных значений х и у по графику, который изображён на рисунке 5.32, а. Какая зависимость связывает координаты точек этой прямой? Запишите её на алгебраическом языке.
б) Выполните аналогичное задание, используя график, изображённый на рисунке 5.32, б.

а) Таблица:
\[
\begin{array}{|c|c|c|c|c|c|}
\hline
x & -2 & -1 & 0 & 1 & 2 \\
\hline
y & -1 & -0{,}5 & 0 & 0{,}5 & 1 \\
\hline
\end{array}
\]\( x = 2y, \quad y = \frac{1}{2}x \).

б) Таблица:
\(\begin{array}{|c|c|c|c|c|}
\hline
x & -2 & -1 & 0 & 1 \\
\hline
y & -1 & 0 & 1 & 2 \\
\hline
\end{array}\)
\( y — x = 1, \quad y = 1 + x \).

а) Таблица:
\[
\begin{array}{|c|c|c|c|c|c|}
\hline
x & -2 & -1 & 0 & 1 & 2 \\
\hline
y & -1 & -0{,}5 & 0 & 0{,}5 & 1 \\
\hline
\end{array}
\]В данной задаче рассматриваются два взаимосвязанных уравнения:
первое, \( x = 2y \), задает зависимость между переменными \( x \) и \( y \), при этом переменная \( x \) в два раза больше переменной \( y \).
Второе уравнение, \( y = \frac{1}{2}x \), показывает, что переменная \( y \) является половиной от значения переменной \( x \).
Для каждой из этих переменных были вычислены значения, которые приведены в таблице. Таким образом, значения переменной \( y \) рассчитаны для различных значений \( x \) согласно данным уравнениям. Таблица демонстрирует, как изменяется значение \( y \) при изменении \( x \).

б) Таблица:
\(\begin{array}{|c|c|c|c|c|}
\hline
x & -2 & -1 & 0 & 1 \\
\hline
y & -1 & 0 & 1 & 2 \\
\hline
\end{array}\)
Во втором случае мы имеем два других уравнения, которые связывают \( x \) и \( y \):
первое, \( y — x = 1 \), определяет разницу между переменными \( y \) и \( x \), которая всегда равна 1.
Это означает, что значение \( y \) на 1 больше, чем значение \( x \).
Второе уравнение, \( y = 1 + x \), является прямой зависимостью, где значение \( y \) всегда больше значения \( x \) на 1.
Все возможные значения переменной \( y \) вычислены для заданных значений \( x \) и отображены в таблице. Таким образом, можно увидеть, как переменная \( y \) изменяется относительно \( x \), при этом соблюдается линейная зависимость.