ГДЗ по Алгебре 7 Класс Номер 474 Дорофеев, Суворова — Подробные Ответы

Постройте на координатной плоскости и опишите на алгебраическом языке прямую, симметричную точкам прямой х = 3:
а) относительно оси ординат;
б) относительно прямой х = 1.

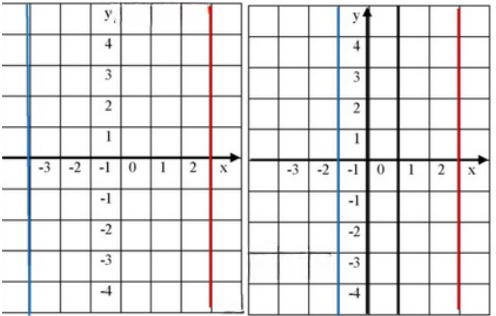
а) \( x = 3 \) — это вертикальная прямая, проходящая через точку \( x = 3 \) на оси \( x \). Симметричная прямая относительно оси ординат будет расположена на таком же расстоянии от оси \( y \), но с противоположным знаком по оси \( x \). Таким образом, симметричная прямая будет проходить через точку \( x = -3 \), и её уравнение будет записано как \( x = -3 \). Это вертикальная прямая, симметричная относительно оси ординат.

б) Прямая \(x=-1\) получается из прямой \(x=3\) отражением относительно прямой \(x=1\), так как расстояние от \(x=3\) до \(x=1\) равно 2, и такое же расстояние откладываем влево от \(x=1\): \(1-2=-1\).

а) \( x = 3 \) — это вертикальная прямая, которая проходит через точку \( x = 3 \) на оси \( x \) и параллельна оси \( y \). Прямая \( x = 3 \) представляет собой набор всех точек на координатной плоскости, у которых значение \( x \) равно 3, а значение \( y \) может быть любым. Это вертикальная линия, которая не пересекает ось \( x \), так как её координата по оси \( x \) фиксирована и равна 3. Симметричная прямая относительно оси ординат будет находиться на таком же расстоянии от оси \( y \), но с противоположным знаком по оси \( x \). Таким образом, симметричная прямая будет проходить через точку \( x = -3 \), и её уравнение будет записано как \( x = -3 \). Это также вертикальная прямая, расположенная симметрично по отношению к оси \( y \) и делящая плоскость на две части, с противоположными знаками по оси \( x \).

б) Симметрия прямой \(x=3\) относительно прямой \(x=1\) означает, что прямая-образ должна располагаться на таком же расстоянии от оси симметрии, но по другую сторону. Прямая \(x=3\) вертикальная и проходит через все точки с абсциссой \(3\), то есть через точки \((3; y)\) для любых значений \(y\). Ось симметрии тоже вертикальная, это прямая \(x=1\), проходящая через точки \((1; y)\).

Рассмотрим расстояние между прямыми \(x=3\) и \(x=1\) по оси \(x\). Оно равно разности их абсцисс: \(3-1=2\). Значит, каждая точка прямой \(x=3\) находится на расстоянии \(2\) единицы справа от оси симметрии \(x=1\). При отражении точки относительно вертикальной прямой её ордината \(y\) не меняется, а абсцисса смещается на такое же расстояние в противоположную сторону. Поэтому абсцисса любой точки-образа будет равна \(1-2=-1\).

Следовательно, все образы точек прямой \(x=3\) имеют координаты \((-1; y)\), где значение \(y\) остаётся тем же, что и у исходных точек. Это означает, что после отражения получается вертикальная прямая с уравнением \(x=-1\). Такая прямая находится на расстоянии \(2\) единицы слева от оси \(x=1\), то есть симметрична прямой \(x=3\) относительно прямой \(x=1\).