ГДЗ по Алгебре 7 Класс Номер 469 Дорофеев, Суворова — Подробные Ответы

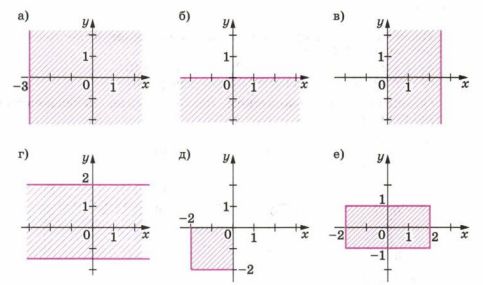
Опишите на алгебраическом языке области координатной плоскости, изображённые на рисунке 5.26, a—е.

a) \(x\ge -3\).

б) \( y \leq 0 \);

в) \( 0 < x \leq 2.5 \);

г) \( -1.5 \leq y \leq 2 \);

д) \( -2 \leq x \leq 0 \) и \( -2 \leq y \leq 0 \);

е) \( -2 \leq x \leq 2 \) и \( -1 \leq y \leq 1 \);

a) На рисунке a) проведена вертикальная прямая \(x=-3\). Эта прямая является границей заштрихованной области: она выделена цветом и входит в область, то есть все точки на самой линии тоже считаются подходящими. Заштрихована вся часть координатной плоскости, которая расположена справа от этой прямой. Для любой точки этой области первая координата \(x\) не может быть меньше \(-3\): если точка была бы левее, то её x был бы меньше \(-3\) и она оказалась бы вне заштрихованной части. Значит, условие принадлежности точки к области можно записать как неравенство \(x\ge -3\). Это неравенство описывает всю полуплоскость справа от прямой \(x=-3\) вместе с самой этой прямой.

б) \( y \leq 0 \) — это область на координатной плоскости, которая расположена ниже горизонтальной прямой \( y = 0 \), включая саму прямую. Это означает, что все точки, у которых \( y \) меньше либо равно нулю, принадлежат этой области. Геометрически это полуплоскость, расположенная ниже оси \( x \), включая саму ось. В этой области значение по оси \( y \) будет отрицательным или равным нулю, а значение по оси \( x \) может быть любым.

в) \( 0 < x \leq 2.5 \) — это область на координатной плоскости, которая расположена между вертикальными прямыми \( x = 0 \) и \( x = 2.5 \). Эти прямые включены в область, так как неравенство \( \leq \) предполагает, что точка на прямой \( x = 2.5 \) также удовлетворяет условию. Таким образом, эта область включает все точки с координатами \( x \), которые находятся между 0 и 2.5, а значения по оси \( y \) могут быть любыми. Это прямоугольная область, расположенная между вертикальными прямыми и вдоль всей оси \( y \).

г) \( -1.5 \leq y \leq 2 \) — это область на координатной плоскости, которая ограничена двумя горизонтальными прямыми \( y = -1.5 \) и \( y = 2 \). Эти прямые включены в область, так как неравенства \( \leq \) и \( \geq \) позволяют точкам на этих прямых быть частью множества. Все точки, для которых значение \( y \) лежит между -1.5 и 2, а значение \( x \) может быть любым, принадлежат этой области. Это горизонтальная полоса, ограниченная прямыми на уровне \( y = -1.5 \) и \( y = 2 \).

д) \( -2 \leq x \leq 0 \) и \( -2 \leq y \leq 0 \) — это прямоугольная область, ограниченная прямыми \( x = -2 \), \( x = 0 \), \( y = -2 \) и \( y = 0 \). Эти прямые включены в область, так как неравенства \( \leq \) позволяют точки на этих прямых быть частью множества. Все точки, которые лежат между этими прямыми и для которых значения \( x \) лежат в пределах от -2 до 0, а значения \( y \) — от -2 до 0, принадлежат этой области. Это прямоугольник с вершинами в точках \( (-2, -2) \), \( (0, -2) \), \( (-2, 0) \) и \( (0, 0) \), включая все его внутренние точки и границы.

е) \( -2 \leq x \leq 2 \) и \( -1 \leq y \leq 1 \) — это область на координатной плоскости, ограниченная прямыми \( x = -2 \), \( x = 2 \), \( y = -1 \) и \( y = 1 \). Эти прямые включены в область, так как неравенства \( \leq \) и \( \geq \) предполагают, что точки на этих прямых также принадлежат множеству. Эта область является прямоугольником с вершинами в точках \( (-2, -1) \), \( (2, -1) \), \( (-2, 1) \) и \( (2, 1) \), включая все его внутренние точки и границы. Все точки внутри этой области удовлетворяют указанным условиям для \( x \) и \( y \).