ГДЗ по Алгебре 7 Класс Номер 467 Дорофеев, Суворова — Подробные Ответы

Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют двойному неравенству:
a) \(-12<x<8\);
б) \(1{,}5<y<2\);
в) \(-5{,}5<x<-5\);
г) \(-0{,}5 \le y \le 1{,}5\).

а

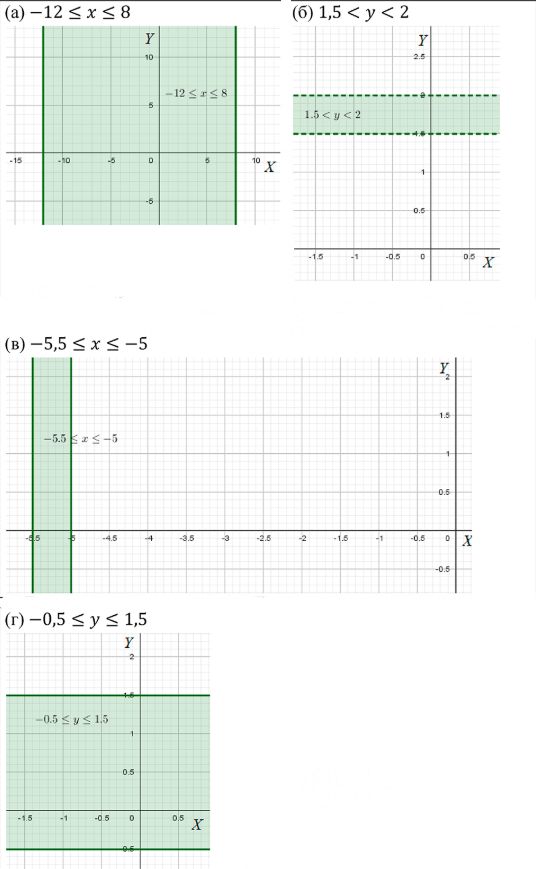
a) Отмечаем на оси \(x\) точки \(-12\) и \(8\), проводим через них вертикальные прямые. Закрашиваем всю полосу между ними, включая границы, так как неравенство \(-12 \le x \le 8\).

б) Отмечаем на оси \(y\) точки \(1{,}5\) и \(2\), проводим через них горизонтальные прямые. Закрашиваем полосу между ними, не закрашивая сами прямые, так как неравенство \(1{,}5 < y < 2\).

в) Отмечаем на оси \(x\) точки \(-5{,}5\) и \(-5\), проводим через них вертикальные прямые. Закрашиваем узкую вертикальную полосу между ними, включая границы, так как неравенство \(-5{,}5 \le x \le -5\).

г) Отмечаем на оси \(y\) точки \(-0{,}5\) и \(1{,}5\), проводим через них горизонтальные прямые. Закрашиваем полосу между ними, включая границы, так как неравенство \(-0{,}5 \le y \le 1{,}5\).

a) Неравенство \(-12 \le x \le 8\) описывает все точки координатной плоскости, у которых горизонтальная координата \(x\) лежит между числами \(-12\) и \(8\), включая сами эти значения. Сначала на оси \(x\) находим и отмечаем точки \(-12\) и \(8\). Через каждую из этих точек проводим вертикальную прямую: через \(-12\) слева и через \(8\) справа. Так как стоят знаки \(\le\), эти прямые входят в решение, поэтому на рисунке границы показывают сплошными линиями. Далее закрашиваем всю область между этими двумя вертикальными линиями по всей высоте координатной плоскости (вверх и вниз от оси \(x\)), поскольку для любой точки из закрашенной полосы координата \(x\) удовлетворяет условию \(-12 \le x \le 8\). Таким образом, решение представляет собой бесконечную по вертикали полосу, ограниченную двумя вертикальными прямыми.

б) Неравенство \(1{,}5 < y < 2\) задаёт множество точек, у которых вертикальная координата \(y\) находится строго между числами \(1{,}5\) и \(2\), при этом сами значения \(1{,}5\) и \(2\) не входят в решение. На оси \(y\) отмечаем точки \(1{,}5\) и \(2\). Через них проводим горизонтальные прямые: одна на уровне \(y = 1{,}5\), другая на уровне \(y = 2\). Поскольку неравенства строгие (знаки \(<\)), линии-граничные значения в теории не входят в решение; на рисунке это обычно подчёркивается пунктиром или иным визуальным отличием, однако основная идея: искомая область находится между этими двумя прямыми. Затем закрашиваем всю полосу между прямыми по всей ширине координатной сетки, так как значение \(x\) может быть любым, ограничение наложено только на \(y\). В результате получаем горизонтальную «ленту», где каждая точка удовлетворяет условию \(1{,}5 < y < 2\).

в) В неравенстве \(-5{,}5 \le x \le -5\) снова ограничивается координата \(x\), но теперь отрезок очень узкий: от \(-5{,}5\) до \(-5\), причём оба конца входят в решение из-за знака \(\le\). На оси \(x\) находим точки \(-5{,}5\) и \(-5\). Через них проводим две вертикальные прямые. Так как обе границы включены, они считаются частью решения и на рисунке изображаются сплошными. Далее закрашиваем пространство между этими прямыми, получая очень узкую вертикальную полоску, которая простирается на всём видимом участке по оси \(y\) (вверх и вниз). Любая точка из этой полосы имеет координату \(x\) в интервале \([-5{,}5; -5]\), а координата \(y\) может быть любой, что как раз и соответствует заданному двойному неравенству.

г) Неравенство \(-0{,}5 \le y \le 1{,}5\) ограничивает вертикальную координату \(y\), причём обе границы включены. Отмечаем на оси \(y\) точки \(-0{,}5\) и \(1{,}5\). Через каждую из них проводим горизонтальную прямую: нижнюю на уровне \(y = -0{,}5\) и верхнюю на уровне \(y = 1{,}5\). Поскольку стоит знак \(\le\), эти прямые входят в множество решений и показываются сплошными линиями. Далее закрашиваем всю область между ними по всей ширине координатной плоскости: координата \(x\) может быть любой, но \(y\) обязан удовлетворять \(-0{,}5 \le y \le 1{,}5\). В итоге получается горизонтальная полоса, ограниченная двумя сплошными линиями, которая и является геометрическим образом всех решений данного двойного неравенства.