ГДЗ по Алгебре 7 Класс Номер 466 Дорофеев, Суворова — Подробные Ответы

а) \( x > 5 \);

б) \( x \leq \frac{2}{5} \);

в) \( x > 0 \);

г) \( y \geq -2 \);

д) \( y > 0 \);

е) \( y > -3.5 \);

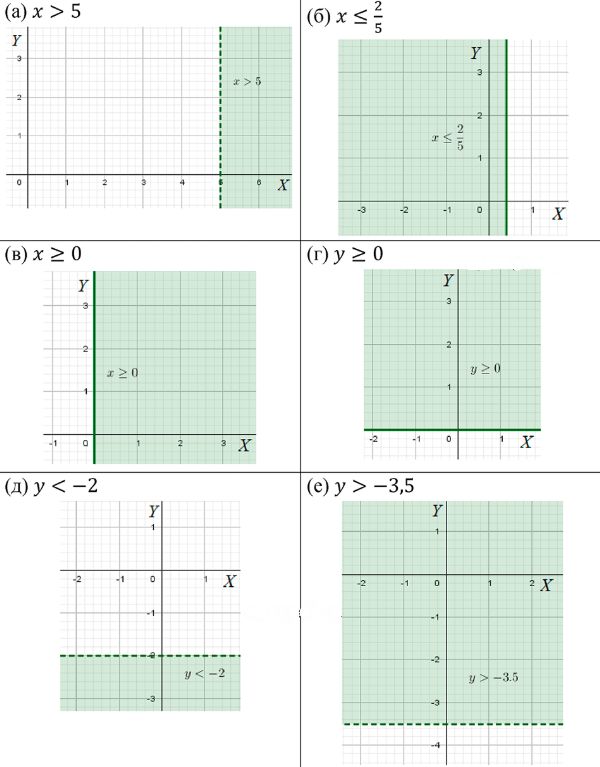
а) \( x > 5 \) — область, расположенная справа от вертикальной прямой \( x = 5 \), не включая саму прямую.

б) \( x \leq \frac{2}{5} \) — область, расположенная слева от вертикальной прямой \( x = \frac{2}{5} \), включая саму прямую.

в) \( x \geq 0 \) — область, расположенная справа от оси \( y \), включая саму ось.

г) \( y \geq 0 \) — область, расположенная выше оси \( x \), включая саму ось.

д) \( y < -2 \) — область, расположенная ниже горизонтальной прямой \( y = -2 \), не включая саму прямую.

е) \( y > -3.5 \) — область, расположенная выше горизонтальной прямой \( y = -3.5 \), не включая саму прямую.

а) \( x > 5 \) — это область на координатной плоскости, которая расположена справа от вертикальной прямой \( x = 5 \). Она включает все точки, для которых значение координаты \( x \) больше 5. Эта область не включает саму прямую \( x = 5 \), так как неравенство строгое (\( x > 5 \)). Прямая \( x = 5 \) является границей, за которой начинается область, и все точки, расположенные вправо от этой прямой, удовлетворяют данному условию. Эти точки могут иметь любые значения по оси \( y \), но обязательно \( x > 5 \).

б) \( x \leq \frac{2}{5} \) — это область, расположенная слева от вертикальной прямой \( x = \frac{2}{5} \), включая саму прямую. В этой области все точки удовлетворяют условию, что \( x \) не больше или равно \( \frac{2}{5} \). Это значит, что любые точки, расположенные на прямой \( x = \frac{2}{5} \) или слева от неё, входят в множество, в том числе и сама прямая. Такие точки могут иметь любые значения по оси \( y \), но их значение по оси \( x \) будет ограничено \( x \leq \frac{2}{5} \).

в) \( x \geq 0 \) — это область на координатной плоскости, которая расположена справа от оси \( y \), включая саму ось. Для всех точек в этой области значение \( x \) будет больше или равно нулю, то есть все точки на правой части координатной плоскости, а также сама ось \( y \) (где \( x = 0 \)), удовлетворяют данному условию. Эти точки могут иметь любые значения по оси \( y \), но их значение по оси \( x \) всегда будет неотрицательным, то есть \( x \geq 0 \).

г) \( y \geq 0 \) — это область, расположенная выше оси \( x \), включая саму ось. Все точки, которые лежат в верхней половине координатной плоскости, а также сама ось \( x \), удовлетворяют данному условию. Для всех этих точек значение \( y \) будет больше или равно нулю, то есть все точки, расположенные выше или на оси \( x \), будут принадлежать этой области. Эти точки могут иметь любые значения по оси \( x \), но их значение по оси \( y \) всегда будет неотрицательным, то есть \( y \geq 0 \).

д) \( y < -2 \) — это область, расположенная ниже горизонтальной прямой \( y = -2 \), не включая саму прямую. Все точки, расположенные ниже этой прямой, где \( y \) строго меньше -2, удовлетворяют данному условию. Эти точки могут иметь любые значения по оси \( x \), но значение \( y \) будет строго меньше -2. Прямая \( y = -2 \) является границей, и все точки, расположенные ниже неё, входят в область решения.

е) \( y > -3.5 \) — это область, расположенная выше горизонтальной прямой \( y = -3.5 \), не включая саму прямую. Все точки, расположенные выше этой прямой, где значение \( y \) больше чем -3.5, удовлетворяют данному условию. Эти точки могут иметь любые значения по оси \( x \), но их значение по оси \( y \) всегда будет строго больше -3.5. Прямая \( y = -3.5 \) является границей, и все точки, расположенные выше неё, принадлежат области решения.