ГДЗ по Алгебре 7 Класс Номер 461 Дорофеев, Суворова — Подробные Ответы

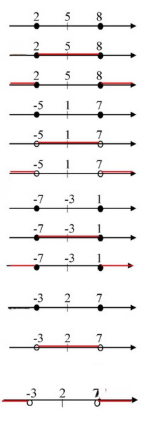
Изобразите на координатной прямой множество точек, удовлетворяющих условиям:
а) \(|x-5|=3,\ |x-5|<3,\ |x-5|>3;\)
б) \(|x-1|=6,\ |x-1|<6,\ |x-1|>6;\)
в) \(|x+3|=4,\ |x+3|<4,\ |x+3|>4;\)
г) \(|x+2|=5,\ |x+2|<5,\ |x+2|>5\).

a) \(|x-5|=3\).
Решаем: \(x-5=3\) или \(x-5=-3\). Тогда \(x=8\) или \(x=2\).

\(|x-5|\le3\).
\(x-5\le3\) и \(x-5\ge-3\). Получаем \(2\le x\le8\).

\(|x-5|\ge3\).
\(x-5\ge3\) или \(x-5\le-3\). Тогда \(x\ge8\) или \(x\le2\).

б) \(|x-1|=6\).
\(x-1=6\) или \(x-1=-6\). Тогда \(x=7\) или \(x=-5\).

\(|x-1|<6\).
\(-6<x-1<6\). Тогда \(-5<x<7\).

\(|x-1|>6\).
\(x-1>6\) или \(x-1<-6\). Тогда \(x>7\) или \(x<-5\).

в) \(|x+3|=4\).
\(x+3=4\) или \(x+3=-4\). Тогда \(x=1\) или \(x=-7\).

\(|x+3|\le4\).
\(-4\le x+3\le4\). Тогда \(-7\le x\le1\).

\(|x+3|\ge4\).
\(x+3\ge4\) или \(x+3\le-4\). Тогда \(x\ge1\) или \(x\le-7\).

г) \(|x+2|=5\).
\(x+2=5\) или \(x+2=-5\). Тогда \(x=3\) или \(x=-7\).

\(|x+2|<5\).
\(-5<x+2<5\). Тогда \(-7<x<3\).

\(|x+2|>5\).
\(x+2>5\) или \(x+2<-5\). Тогда \(x>3\) или \(x<-7\).

a) Рассмотрим выражение \(|x-5|\). Это расстояние числа \(x\) от числа \(5\) на числовой прямой. Уравнение \(|x-5|=3\) означает, что расстояние от \(x\) до \(5\) равно \(3\). Расстояние на прямой всегда неотрицательно, поэтому мы записываем два случая: \(x-5=3\) и \(x-5=-3\). В первом случае \(x=5+3=8\), во втором \(x=5-3=2\). Значит, все числа \(x\), удовлетворяющие условию, это \(x=2\) и \(x=8\); они на расстоянии \(3\) единицы от точки \(5\).

Неравенство \(|x-5|\le3\) означает, что расстояние между \(x\) и \(5\) не больше \(3\), то есть точка \(x\) расположена на числовой прямой не дальше чем на \(3\) единицы вправо или влево от \(5\). По определению модуля получаем двойное неравенство: \(-3\le x-5\le3\). Прибавляя к каждой части \(5\), получаем \(2\le x\le8\). Это отрезок от \(2\) до \(8\), включая концы, потому что знак нестрогий (\(\le\)).

Неравенство \(|x-5|\ge3\) означает, что расстояние от \(x\) до \(5\) не меньше \(3\). Тогда точка \(x\) лежит либо правее точки \(8\), либо левее точки \(2\), потому что сами точки \(2\) и \(8\) как раз на расстоянии \(3\) от \(5\). Записываем по определению модуля: \(x-5\ge3\) или \(x-5\le-3\). В первом случае \(x\ge8\), во втором \(x\le2\). Получаем два луча: \(x\le2\) и \(x\ge8\); все такие \(x\) находятся не ближе чем на \(3\) единицы от точки \(5\).

б) Выражение \(|x-1|\) показывает расстояние числа \(x\) от числа \(1\). Уравнение \(|x-1|=6\) означает, что расстояние от точки \(x\) до точки \(1\) равно \(6\). Записываем два случая: \(x-1=6\) и \(x-1=-6\), так как модуль равен числу, если выражение внутри может быть как положительным, так и отрицательным. В первом случае \(x=1+6=7\), во втором \(x=1-6=-5\). Следовательно, \(x=-5\) и \(x=7\) — это точки, которые находятся на расстоянии \(6\) единиц от \(1\).

Неравенство \(|x-1|<6\) означает, что расстояние от \(x\) до \(1\) строго меньше \(6\). Тогда \(x\) лежит внутри интервала длиной \(12\), центрированного в точке \(1\). Формально по определению модуля: \(-6<x-1<6\). Прибавляем \(1\) ко всем частям: \(-5<x<7\). Это открытый интервал от \(-5\) до \(7\): концы \(-5\) и \(7\) не входят, так как при них модуль становится равным \(6\), а нам нужно строго меньше \(6\).

Неравенство \(|x-1|>6\) означает, что расстояние от \(x\) до \(1\) строго больше \(6\), то есть точки, расположенные дальше, чем \(-5\) и \(7\). По определению: \(x-1>6\) или \(x-1<-6\). Решаем каждое: из \(x-1>6\) получаем \(x>7\); из \(x-1<-6\) получаем \(x<-5\). Значит, множество решений состоит из двух лучей: \(x<-5\) и \(x>7\). Точки \(-5\) и \(7\) не входят, так как там модуль равен \(6\), а нужно больше \(6\).

в) В выражении \(|x+3|\) число внутри модуля можно представить как расстояние числа \(x\) от числа \(-3\), потому что \(x+3=x-(-3)\). Уравнение \(|x+3|=4\) значит, что расстояние от \(x\) до \(-3\) равно \(4\). Записываем два случая: \(x+3=4\) и \(x+3=-4\). В первом случае \(x=4-3=1\), во втором \(x=-4-3=-7\). Значит, решения — это точки \(x=-7\) и \(x=1\), каждая из которых отстоит от точки \(-3\) на \(4\) единицы.

Неравенство \(|x+3|\le4\) говорит, что расстояние от \(x\) до \(-3\) не больше \(4\). Тогда все подходящие точки лежат на отрезке длиной \(8\) с центром в точке \(-3\). По определению модуля имеем \(-4\le x+3\le4\). Вычитаем \(3\) из всех трёх частей: \(-7\le x\le1\). Это отрезок от \(-7\) до \(1\), включая концы, так как при \(x=-7\) и \(x=1\) модуль равен \(4\), что удовлетворяет знаку \(\le\).

Неравенство \(|x+3|\ge4\) означает, что расстояние от \(x\) до \(-3\) не меньше \(4\), то есть точки расположены не ближе чем на \(4\) единицы к \(-3\). Запишем: \(x+3\ge4\) или \(x+3\le-4\). Из первого получаем \(x\ge1\); из второго \(x\le-7\). Таким образом, решения образуют два луча: все \(x\le-7\) и все \(x\ge1\); каждый такой \(x\) не ближе, чем на \(4\) единицы к \(-3\).

г) В выражении \(|x+2|\) мы имеем модуль числа \(x+2\), то есть расстояние числа \(x\) от числа \(-2\), потому что \(x+2=x-(-2)\). Уравнение \(|x+2|=5\) означает, что расстояние от \(x\) до \(-2\) равно \(5\). Запишем два уравнения: \(x+2=5\) и \(x+2=-5\). В первом случае \(x=5-2=3\), во втором \(x=-5-2=-7\). Следовательно, решения уравнения — \(x=-7\) и \(x=3\), обе точки по \(5\) единиц от центра \(-2\).

Неравенство \(|x+2|<5\) означает, что расстояние от \(x\) до \(-2\) строго меньше \(5\), то есть \(x\) лежит внутри интервала, ограниченного точками \(-7\) и \(3\). По определению модуля: \(-5<x+2<5\). Вычитаем \(2\) из всех частей: \(-7<x<3\). Это открытый интервал, концы \(-7\) и \(3\) не входят, так как при них модуль равен \(5\), а нам нужно меньше \(5\).

Неравенство \(|x+2|>5\) означает, что расстояние от \(x\) до \(-2