ГДЗ по Алгебре 7 Класс Номер 449 Дорофеев, Суворова — Подробные Ответы

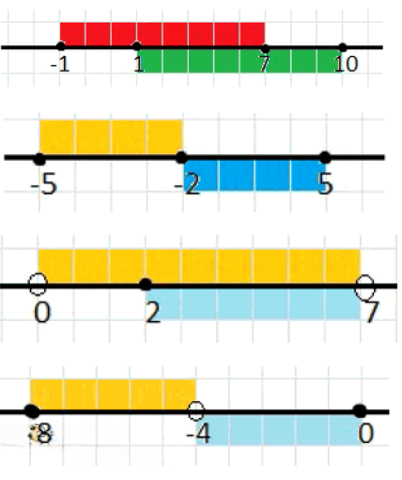
Изобразите на координатной прямой указанные промежутки (используйте для этого разные цветные карандаши). Найдите объединение и пересечение этих промежутков:

а) \(-1\le x\le 7\); \(1\le x\le 10\)

б) \(-5\le x\le -2\); \(-2\le x\le 5\)

в) \(0<x<7\); \(2\le x<7\)

г) \(-8\le x<-4\); \(-4<x\le 0\)

a) \(x\in[-1,7]\) и \(x\in[1,10]\). Объединение берём от меньшей левой границы до большей правой: \(x\in[-1,10]\). Пересечение — общая часть: \(x\in[1,7]\).

б) \(x\in[-5,-2]\) и \(x\in[-2,5]\). Объединение: \(x\in[-5,5]\). Пересечение — общая точка \(x=-2\), то есть \(x=-2\).

в) \(x\in(0,7)\) и \(x\in[2,7)\). Так как \([2,7)\subset(0,7)\), объединение: \(x\in(0,7)\). Пересечение: \(x\in[2,7)\).

г) \(x\in[-8,-4)\) и \(x\in(-4,0]\). Точка \(-4\) не входит ни в один промежуток, поэтому пересечения нет: \(x\in\emptyset\). Объединение: \(x\in[-8,0]\).

a) Даны два отрезка: \(x\in[-1,7]\) и \(x\in[1,10]\). Объединение — это все значения \(x\), которые попадают хотя бы в один из промежутков. Первый отрезок покрывает числа от \(-1\) до \(7\) включительно, второй — от \(1\) до \(10\) включительно, и они перекрываются на участке от \(1\) до \(7\), значит вместе они образуют один сплошной отрезок от самой левой точки \(-1\) до самой правой точки \(10\): \(x\in[-1,10]\).

a) Пересечение — это только те значения \(x\), которые одновременно принадлежат обоим промежуткам. Чтобы число лежало сразу в \([-1,7]\) и в \([1,10]\), оно должно быть не меньше \(1\) (из второго условия) и не больше \(7\) (из первого условия). Концы \(1\) и \(7\) входят в оба отрезка, поэтому пересечение получается отрезком: \(x\in[1,7]\).

б) Даны два отрезка: \(x\in[-5,-2]\) и \(x\in[-2,5]\). Объединение снова означает «хотя бы в одном»: первый отрезок даёт все числа от \(-5\) до \(-2\) включительно, второй — от \(-2\) до \(5\) включительно. Они «стыкуются» в точке \(-2\), причём \(-2\) входит в оба отрезка, значит разрыва нет и общий охват идёт от \(-5\) до \(5\): \(x\in[-5,5]\).

б) Пересечение — «в обоих сразу»: чтобы \(x\) принадлежал \([-5,-2]\), нужно \(x\le -2\), а чтобы принадлежал \([-2,5]\), нужно \(x\ge -2\). Оба условия одновременно выполняются только при \(x=-2\). Так как \(-2\) включён в оба отрезка, пересечение — одна точка: \(x=-2\).

в) Даны промежутки: \(x\in(0,7)\) и \(x\in[2,7)\). В первом случае концы не входят: \(0\) и \(7\) исключены, во втором — \(2\) входит, а \(7\) не входит. Заметим, что любой \(x\) из \([2,7)\) автоматически удовлетворяет условию \(0<x<7\), то есть весь промежуток \([2,7)\) целиком содержится внутри \((0,7)\).

в) Поэтому объединение (хотя бы в одном) не расширяет первый промежуток: всё, что есть во втором, уже лежит в первом, значит объединение остаётся \(x\in(0,7)\). Пересечение (в обоих) как раз и будет тем промежутком, который «общий» для них, то есть меньший из них: \(x\in[2,7)\).

г) Даны промежутки: \(x\in[-8,-4)\) и \(x\in(-4,0]\). В первом \(-8\) входит, а \(-4\) не входит; во втором \(-4\) не входит, а \(0\) входит. Эти промежутки расположены по разные стороны от точки \(-4\), причём сама точка \(-4\) исключена в обоих случаях, значит «склейки» между ними нет.

г) Объединение — это все числа, которые попадают либо в \([-8,-4)\), либо в \((-4,0]\), поэтому запись: \(x\in[-8,-4)\cup(-4,0]\). Пересечение требует, чтобы одно и то же число одновременно было меньше \(-4\) (чтобы попасть в \([-8,-4)\)) и больше \(-4\) (чтобы попасть в \((-4,0]\)), что невозможно, поэтому пересечение пусто: \(x\in\emptyset\).