ГДЗ по Алгебре 7 Класс Номер 441 Дорофеев, Суворова — Подробные Ответы

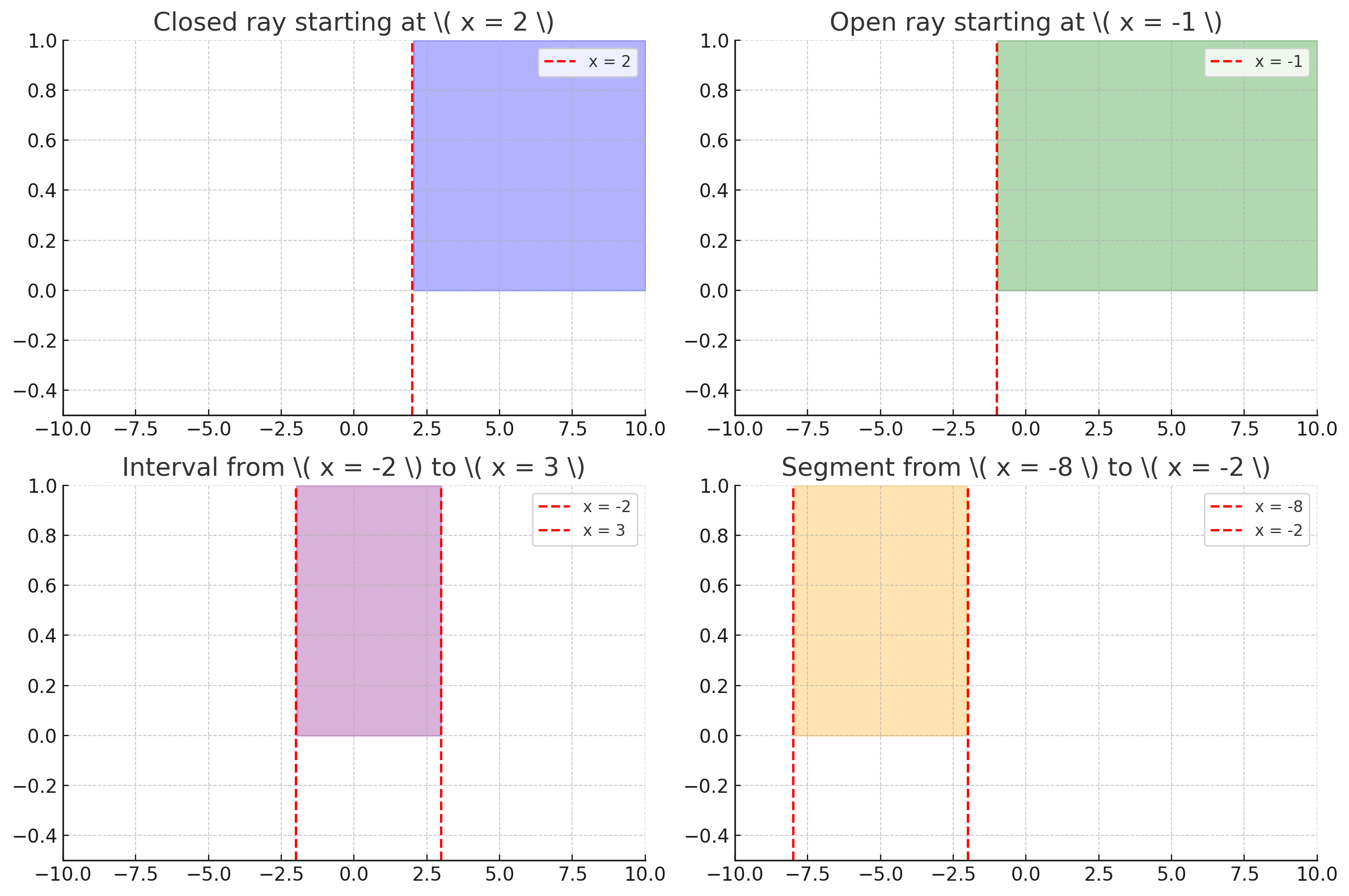
Изобразите на координатной прямой и опишите на алгебраическом языке:
а) замкнутый луч с началом в точке 2 (сколько существует таких лучей?);
б) открытый луч с началом в точке -1 (сколько существует таких лучей?);
в) интервал от точки -2 до точки 3;
г) отрезок с концами в точках -8 и -2.

а) При \(x \ge 2\) получаем луч вправо от точки \(2\) (точка \(2\) включена). При \(x \le 2\) получаем луч влево от точки \(2\) (точка \(2\) включена).

б) При \(x>-1\) получаем луч вправо от точки \(-1\) (точка \(-1\) не включена). При \(x<-1\) получаем луч влево от точки \(-1\) (точка \(-1\) не включена).

в) Неравенство \(-2<x<3\) задаёт интервал между \(-2\) и \(3\) без концов, то есть \((-2;3)\).

г) Неравенство \(-8\le x\le -2\) задаёт отрезок от \(-8\) до \(-2\) с включёнными концами, то есть \([-8;-2]\).

а) В неравенстве \(x\ge 2\) знак «\(\ge\)» означает «больше или равно», то есть подходят все числа, которые либо равны \(2\), либо больше \(2\). На числовой прямой это изображают так: в точке \(2\) ставят закрашенную точку (потому что значение \(2\) входит в решение), а затем проводят луч вправо, так как вправо откладываются числа больше \(2\). Поэтому множество решений — все \(x\), начиная с \(2\) и дальше вправо.

В неравенстве \(x\le 2\) знак «\(\le\)» означает «меньше или равно», то есть подходят все числа, которые либо равны \(2\), либо меньше \(2\). На числовой прямой снова в точке \(2\) ставят закрашенную точку (потому что \(2\) входит в решение), но луч проводят влево, так как влево расположены числа меньше \(2\). Поэтому действительно получается «2 таких луча»: один для \(x\ge 2\), другой для \(x\le 2\).

б) В неравенстве \(x>-1\) знак «\(>\)» означает строгое неравенство: число \(-1\) не подходит, а подходят все числа, которые больше \(-1\). На числовой прямой это показывают пустой (незакрашенной) точкой в \(-1\), потому что точка \(-1\) не включается в решение, и лучом вправо, потому что справа находятся числа, большие \(-1\). То есть берутся все значения \(x\), расположенные правее \(-1\), кроме самой точки \(-1\).

В неравенстве \(x<-1\) знак «\(<\)» тоже строгий: \(-1\) не входит, а подходят все числа меньше \(-1\). Поэтому в точке \(-1\) снова ставят пустую точку, и проводят луч влево, так как слева находятся меньшие числа. Поэтому, как и на фото, здесь существует 2 луча: один вправо для \(x>-1\) и один влево для \(x<-1\), причём \(-1\) нигде не включён.

в) Двойное неравенство \(-2<x<3\) означает одновременное выполнение двух условий: \(x>-2\) и \(x<3\). То есть число \(x\) должно быть строго больше \(-2\), но при этом строго меньше \(3\). На числовой прямой это изображают как выделенный отрезок между точками \(-2\) и \(3\), но обе граничные точки не входят в решение, поэтому в \(-2\) и в \(3\) ставят пустые точки. В итоге получаем интервал \((-2;3)\): все числа между \(-2\) и \(3\), не включая сами \(-2\) и \(3\).

г) Неравенство \(-8\le x\le -2\) также читается как два условия одновременно: \(x\ge -8\) и \(x\le -2\). Здесь границы включаются, потому что стоят знаки «\(\le\)». Значит, подходят все числа, которые лежат между \(-8\) и \(-2\), а также сами числа \(-8\) и \(-2\). На числовой прямой это изображают выделенной частью между \(-8\) и \(-2\) и закрашенными точками в \(-8\) и \(-2\), поскольку эти значения входят в решение. Соответствующее множество решений — отрезок \([-8;-2]\).