ГДЗ по Алгебре 7 Класс Номер 440 Дорофеев, Суворова — Подробные Ответы

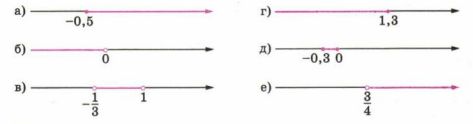
Работаем с символами Опишите на алгебраическом языке промежутки, изображённые на рисунке 5.7, a—е.

а) \( x \geq -0,5 \)

б) \( x < 0 \)

в) \( -\frac{1}{3} < x < 1 \)

г) \( x \leq 1,3 \)

д) \( -0,3 \leq x \leq 0 \)

е) \( x > \frac{3}{4} \)

а) \(x \ge -0{,}5\). Это неравенство читается так: подходят все числа \(x\), которые больше либо равны числу \(-0{,}5\). Знак \(\ge\) означает, что граница \(-0{,}5\) тоже входит в решение, то есть \(x\) может быть ровно \(-0{,}5\) и любым числом правее на числовой прямой. В виде промежутка множество решений записывают так: \(x \in [-0{,}5;\,+\infty)\). Если отмечать на прямой, то в точке \(-0{,}5\) ставят закрашенную точку (граница включена) и проводят луч вправо.

б) \(x < 0\). Здесь подходят все числа, которые строго меньше нуля. Знак \(<\) означает, что само число \(0\) в решения не входит: \(x\) не может быть равен нулю, только меньше него. В виде промежутка это записывают так: \(x \in (-\infty;\,0)\). На числовой прямой в точке \(0\) ставят незакрашенную точку (граница не включена) и проводят луч влево, потому что все подходящие значения находятся левее нуля.

в) \(-\frac{1}{3} < x < 1\). Это двойное неравенство задаёт числа \(x\), которые лежат строго между \(-\frac{1}{3}\) и \(1\). Оба знака строгие (\(<\)), значит ни \(-\frac{1}{3}\), ни \(1\) не входят в множество решений: нельзя брать \(x = -\frac{1}{3}\) и нельзя брать \(x = 1\), можно брать только значения между ними, например \(x=0\), \(x=\frac{1}{2}\), \(x=-\frac{1}{4}\). В виде промежутка решение записывают так: \(x \in \left(-\frac{1}{3};\,1\right)\). На числовой прямой ставят две незакрашенные точки в \(-\frac{1}{3}\) и \(1\) и заштриховывают участок между ними.

г) \(x \le 1{,}3\). Это означает, что \(x\) может быть любым числом, которое меньше либо равно \(1{,}3\). Знак \(\le\) показывает включённую границу: значение \(x=1{,}3\) подходит, как и все числа левее \(1{,}3\) (например, \(1\), \(0\), \(-2\)). В интервальной записи: \(x \in (-\infty;\,1{,}3]\). На числовой прямой в точке \(1{,}3\) ставят закрашенную точку и проводят луч влево.

д) \(-0{,}3 \le x \le 0\). Здесь \(x\) ограничен сразу с двух сторон: он не меньше \(-0{,}3\) и не больше \(0\). Оба знака нестрогие (\(\le\)), поэтому обе границы входят в решение: подходят значения \(x=-0{,}3\) и \(x=0\), а также все числа между ними, например \(x=-0{,}2\), \(x=-0{,}15\). В виде промежутка это: \(x \in [-0{,}3;\,0]\). На числовой прямой точки \(-0{,}3\) и \(0\) отмечают закрашенными и выделяют отрезок между ними.

е) \(x > \frac{3}{4}\). Это неравенство задаёт все числа, которые строго больше \(\frac{3}{4}\). Так как знак строгий (\(>\)), значение \(x=\frac{3}{4}\) не подходит, подходят только числа правее этой точки, например \(1\), \(2\), \(0{,}8\). В интервальной форме: \(x \in \left(\frac{3}{4};\,+\infty\right)\). На числовой прямой в точке \(\frac{3}{4}\) ставят незакрашенную точку и проводят луч вправо.