ГДЗ по Алгебре 7 Класс Номер 438 Дорофеев, Суворова — Подробные Ответы

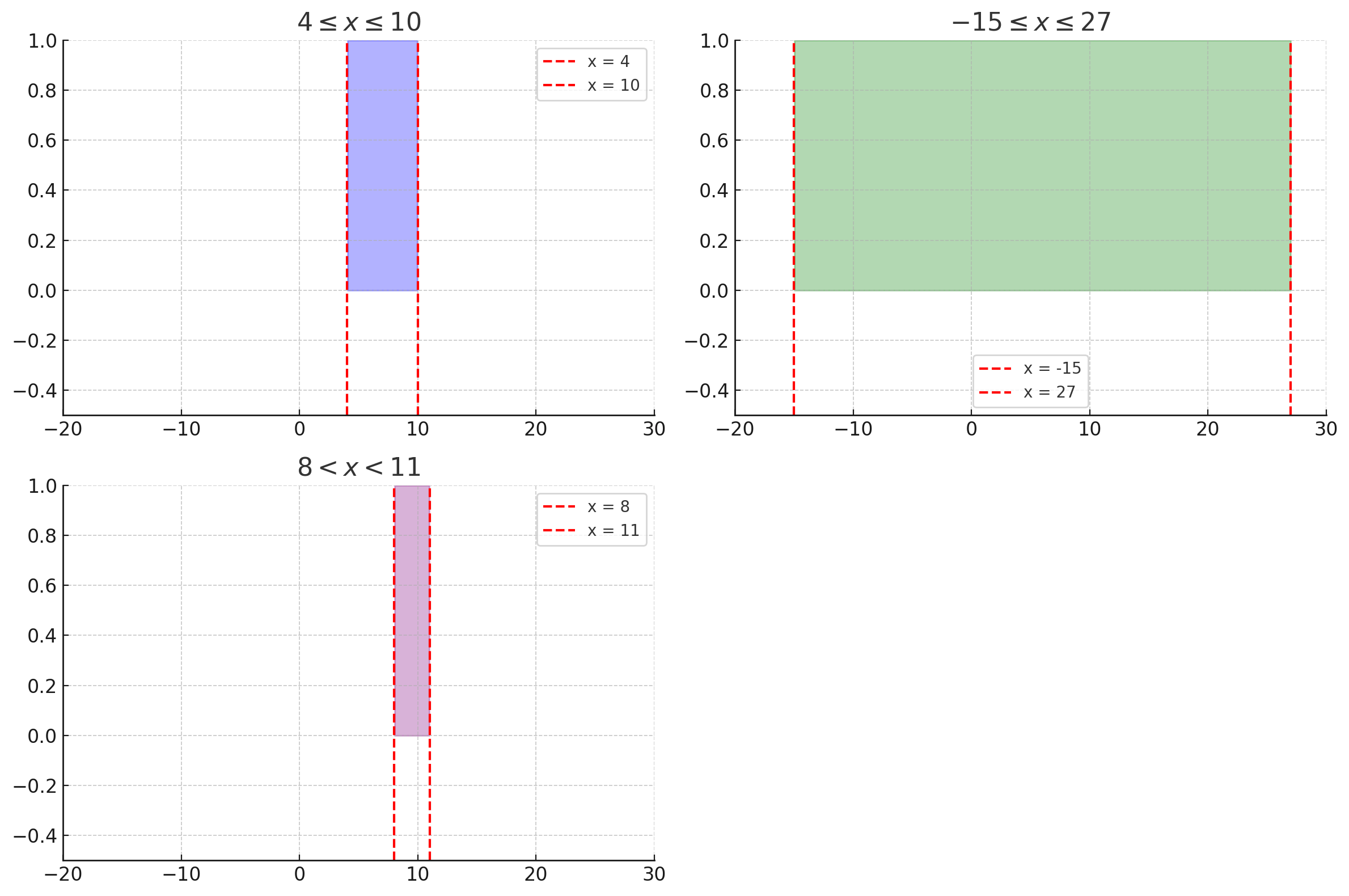
Изобразите на координатной прямой множество точек, координаты которых удовлетворяют двойному неравенству: a) \(4<x<10\); б) \(-15<x<27\); в) \(8<x<11\).

a) Так как \(4\le x\le 10\), подходят все числа от 4 до 10 включительно, на прямой это отрезок \([4;10]\) с закрашенными точками в 4 и 10.

б) Так как \(-15\le x\le 27\), подходят все числа от \(-15\) до 27 включительно, на прямой это отрезок \([-15;27]\) с закрашенными точками в \(-15\) и 27.

в) Так как \(8<x<11\), подходят все числа строго между 8 и 11, на прямой это интервал \((8;11)\) с незакрашенными точками в 8 и 11.

a) Неравенство \(4\le x\le 10\) означает, что число \(x\) может принимать любые значения, которые не меньше 4 и одновременно не больше 10. Знак \(\le\) читается как «меньше или равно», поэтому крайние точки 4 и 10 входят в множество решений.

На координатной прямой это изображают так: отмечают точки 4 и 10, закрашивают их (потому что они включены), а затем проводят сплошной отрезок между ними. Получается множество всех точек от 4 до 10 включительно, то есть отрезок \([4;10]\).

Проверка по смыслу: \(x=4\) подходит, так как \(4\le 4\) и \(4\le 10\); \(x=10\) тоже подходит, так как \(4\le 10\) и \(10\le 10\). Любое число между ними, например \(x=7\), удовлетворяет \(4\le 7\le 10\), значит тоже входит.

б) Неравенство \(-15\le x\le 27\) задаёт все значения \(x\), которые не меньше \(-15\) и не больше 27. Здесь также стоят знаки \(\le\), значит обе границы включены в решение.

На прямой нужно отметить \(-15\) и 27, закрасить эти точки и соединить их отрезком. Это показывает, что подходят все числа на участке от \(-15\) до 27 вместе с концами. В виде промежутка это \([-15;27]\).

Можно понять по примерам: \(x=-15\) удовлетворяет \(-15\le -15\le 27\), \(x=27\) удовлетворяет \(-15\le 27\le 27\), а любое число между ними (например, \(x=0\)) тоже подходит, потому что \(-15\le 0\le 27\).

в) Неравенство \(8<x<11\) означает, что \(x\) должен быть строго больше 8 и строго меньше 11. Знак \(<\) — строгий, поэтому числа 8 и 11 в решение не входят: нельзя брать \(x=8\) и нельзя брать \(x=11\).

На координатной прямой это изображают как интервал между 8 и 11 с пустыми (незакрашенными) кружками в точках 8 и 11. Пустые кружки показывают, что границы не включены, а между ними выделяется линия, показывающая все подходящие значения. В виде промежутка это \((8;11)\).

Для контроля: \(x=8\) не подходит, так как не выполняется \(8<8\); \(x=11\) не подходит, так как не выполняется \(11<11\). Любое число между ними, например \(x=9\) или \(x=10\), подходит, так как \(8<9<11\) и \(8<10<11\).