ГДЗ по Алгебре 7 Класс Номер 436 Дорофеев, Суворова — Подробные Ответы

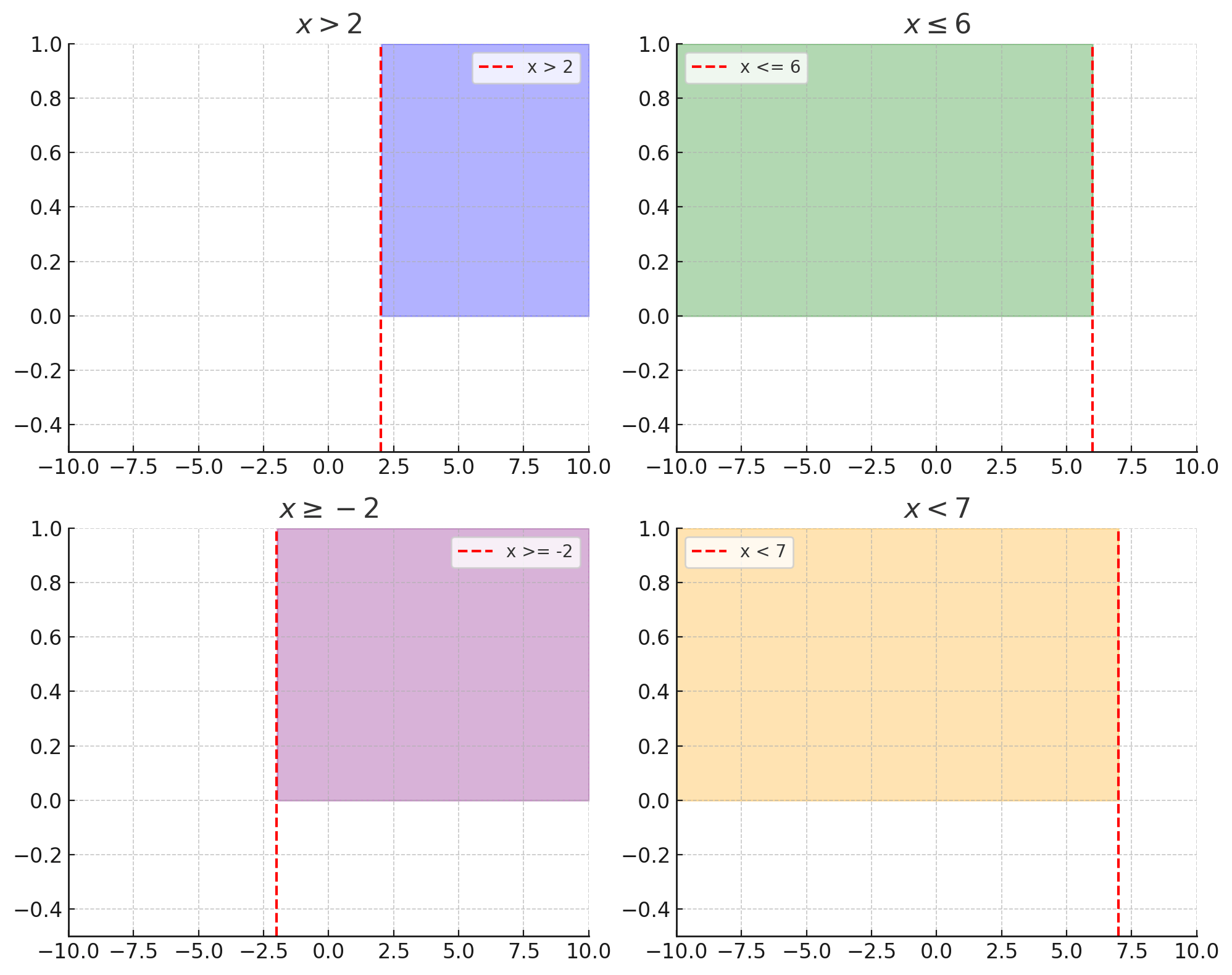
Изобразите на координатной прямой множество точек, заданное неравенством: а) \(x>6\); б) \(x\le 6\); в) \(x\ge -2\); г) \(x<7\). Как называется каждое из этих множеств?

а) Так как \(x>6\), точка \(6\) не входит, на прямой ставим пустую точку в \(6\) и закрашиваем вправо: открытый луч.

б) Так как \(x\le 6\), точка \(6\) входит, на прямой ставим закрашенную точку в \(6\) и закрашиваем влево: замкнутый луч.

в) Так как \(x\ge -2\), точка \(-2\) входит, на прямой ставим закрашенную точку в \(-2\) и закрашиваем вправо: замкнутый луч.

г) Так как \(x<7\), точка \(7\) не входит, на прямой ставим пустую точку в \(7\) и закрашиваем влево: открытый луч.

а) Неравенство \(x>6\) означает: подходят все числа, которые строго больше \(6\). Строгое неравенство показывает, что число \(6\) не является решением, поэтому точка \(6\) на прямой не закрашивается (обозначается пустым кружком). Дальше отмечают все точки правее \(6\), потому что справа располагаются числа больше \(6\).

При изображении на координатной прямой: ставим в точке \(6\) пустой кружок и проводим луч вправо, показывая, что берём все значения \(x\), для которых \(x\) больше \(6\). Такое множество называют открытым лучом, так как начальная точка \(6\) не включена в множество решений.

Дополнительно можно проговорить проверку на примерах: \(x=7\) подходит, потому что \(7>6\); \(x=6\) не подходит, потому что \(6\) не больше \(6\). Значит, на прямой отмечается правая часть от \(6\), но без самой точки \(6\): открытый луч.

б) Неравенство \(x\le 6\) означает: подходят все числа, которые либо меньше \(6\), либо равны \(6\). Знак «\(\le\)» показывает, что точка \(6\) включается в множество решений, поэтому в точке \(6\) ставят закрашенную точку. Так как берутся все числа меньше \(6\), выделяют часть прямой слева от \(6\).

При изображении: отмечаем точку \(6\) закрашенным кружком и проводим луч влево. Это показывает, что множество решений включает и саму границу \(6\), и все значения, расположенные левее. Такое множество называют замкнутым лучом, так как начальная точка \(6\) входит в множество.

Проверка на числах: \(x=6\) подходит, потому что \(6\le 6\); \(x=5\) подходит, потому что \(5\le 6\); \(x=7\) не подходит, потому что \(7\le 6\) неверно. Поэтому закрашено влево от \(6\) вместе с точкой \(6\): замкнутый луч.

в) Неравенство \(x\ge -2\) означает: подходят все числа, которые либо больше \(-2\), либо равны \(-2\). Знак «\(\ge\)» означает включение границы, поэтому точка \(-2\) отмечается закрашенной. Поскольку числа больше \(-2\) находятся правее \(-2\), выделяют правую часть прямой.

На координатной прямой: в точке \(-2\) ставим закрашенную точку и проводим луч вправо. Это означает, что берутся все точки, начиная с \(-2\) и дальше вправо без ограничения. Такое множество называют замкнутым лучом, так как точка \(-2\) включена в решение.

Примеры для контроля: \(x=-2\) подходит, потому что \(-2\ge -2\); \(x=0\) подходит, потому что \(0\ge -2\); \(x=-3\) не подходит, потому что \(-3\ge -2\) неверно. Поэтому закрашиваем \(-2\) и всё правее: замкнутый луч.

г) Неравенство \(x<7\) означает: подходят все числа, которые строго меньше \(7\). Строгость знака «\(<\)» означает, что число \(7\) не входит в множество решений, поэтому точка \(7\) отмечается пустым кружком. Числа меньше \(7\) расположены слева от \(7\), значит выделяется левая часть прямой.

На прямой: ставим в точке \(7\) пустой кружок и проводим луч влево, показывая все значения \(x\), расположенные левее \(7\). Такое множество называют открытым лучом, поскольку граничная точка \(7\) не включена.

Проверка: \(x=6\) подходит, потому что \(6<7\); \(x=7\) не подходит, потому что \(7<7\) неверно; \(x=8\) не подходит, потому что \(8<7\) неверно. Следовательно, закрашивается всё слева от \(7\), но без точки \(7\): открытый луч.