ГДЗ по Алгебра 7 Класс Номер 191 Дорофеев, Суворова — Подробные Ответы

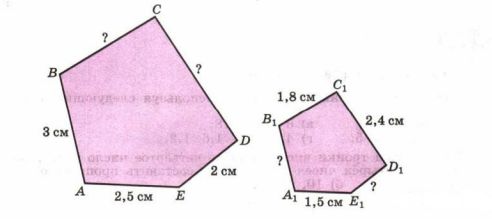
На рисунке 2.10 фигура \( A_1B_1C_1D_1E_1 \) является копией фигуры \( ABCDE \), полученной с помощью копировальной машины, которая уменьшает все размеры в одно и то же число раз.

а) Найдите неизвестные длины сторон.

б) Дополните равенства так, чтобы получились пропорции:

\( \frac{AB}{A_1B_1} = \frac{AE}{A_1E_1} = \frac{BC}{B_1C_1} = \frac{CD}{C_1D_1} \)

в) Найдите отношение периметров этих фигур.

а) Отношение соответствующих сторон: \(1{,}5 : 2{,}5 = 15 : 25 = \frac{15}{25} = \frac{3}{5}\), размеры фигуры \(A_1B_1C_1D_1E_1\) уменьшены в \(\frac{3}{5}\) раза.

\(C_1D_1 : CD = \frac{3}{5}\)

\(CD = C_1D_1 : \frac{3}{5}\)

\(CD = 2{,}4 : \frac{3}{5} = 0{,}8 \cdot 5 = 4\) см

\(C_1B_1 : CB = \frac{3}{5}\)

\(CB = C_1B_1 : \frac{3}{5}\)

\(CB = 1{,}8 : \frac{3}{5} = 0{,}6 \cdot 5 = 3\) см

\(A_1B_1 : AB = \frac{3}{5}\)

\(A_1B_1 = AB \cdot \frac{3}{5}\)

\(A_1B_1 = 3 \cdot \frac{3}{5} = \frac{9}{5} = 1{,}8\) см

\(D_1E_1 : DE = \frac{3}{5}\)

\(D_1E_1 = DE \cdot \frac{3}{5}\)

\(D_1E_1 = 2 \cdot \frac{3}{5} = \frac{6}{5} = 1{,}2\) см

б) \(\frac{AB}{A_1B_1} = \frac{AE}{A_1E_1}\),

\(\frac{AB}{BC} = \frac{A_1B_1}{B_1C_1}\),

\(\frac{DE}{CD} = \frac{D_1E_1}{C_1D_1}\).

в) \(P_{ABCDE} : P_{A_1B_1C_1D_1E_1} =\)
\(= (3+3+4+2+2{,}5):(1{,}8+1{,}8+2{,}4+1{,}2+1{,}5) = 14{,}5 : 8{,}7 = \frac{145}{87} =\)
\(= \frac{5}{3}\).

а) Сначала находим коэффициент уменьшения фигуры, сравнивая соответствующие стороны: берём данные из условия \(1{,}5\) см и \(2{,}5\) см. Составляем отношение \(1{,}5 : 2{,}5\). Чтобы избавиться от запятых, умножаем обе части на \(10\), получаем \(15 : 25\). Это отношение равно дроби \(\frac{15}{25}\). Сокращаем дробь, деля числитель и знаменатель на \(5\): \(\frac{15}{25} = \frac{3}{5}\). Значит, каждая сторона меньшей фигуры \(A_1B_1C_1D_1E_1\) составляет \(\frac{3}{5}\) от соответствующей стороны большей фигуры, то есть размеры уменьшены в \(\frac{3}{5}\) раза. Это ключевой коэффициент подобия: все соответствующие стороны подобны с отношением \(\frac{3}{5}\) (малая к большой) и, наоборот, \(\frac{5}{3}\) (большая к малой).

Далее вычисляем неизвестные стороны. Пусть даны отрезки меньшей фигуры, например \(C_1D_1 = 2{,}4\) см, а нужно найти соответствующую сторону большой фигуры \(CD\). По подобию фигур выполняется отношение \(C_1D_1 : CD = \frac{3}{5}\). Это значит, что меньшая сторона составляет \(\frac{3}{5}\) от большей. Нам нужно выразить \(CD\). Записываем: \(CD = C_1D_1 : \frac{3}{5}\). Деление на дробь заменяем умножением на обратную дробь: \(CD = 2{,}4 \cdot \frac{5}{3}\). Сначала умножаем \(2{,}4\) на \(\frac{1}{3}\): \(2{,}4 : 3 = 0{,}8\). Затем \(0{,}8 \cdot 5 = 4\) см. Значит, \(CD = 4\) см. Аналогично для стороны \(CB\): по условию меньшая сторона \(C_1B_1 = 1{,}8\) см, а большая \(CB\) неизвестна. Отношение такое же: \(C_1B_1 : CB = \frac{3}{5}\). Тогда \(CB = C_1B_1 : \frac{3}{5} = 1{,}8 \cdot \frac{5}{3}\). Делим \(1{,}8\) на \(3\): получаем \(0{,}6\). Умножаем \(0{,}6\) на \(5\): \(0{,}6 \cdot 5 = 3\) см. Значит, \(CB = 3\) см.

Теперь рассмотрим нахождение сторон меньшей фигуры по известным сторонам большей. Для отрезка \(AB\) известно, что большая сторона равна \(AB = 3\) см, а меньшая \(A_1B_1\) неизвестна. Коэффициент подобия тот же: \(A_1B_1 : AB = \frac{3}{5}\). Подставляем \(AB = 3\): \(A_1B_1 = AB \cdot \frac{3}{5} = 3 \cdot \frac{3}{5}\). Перемножаем: \(3 \cdot 3 = 9\), получаем \(A_1B_1 = \frac{9}{5} = 1{,}8\) см. Аналогично для отрезка \(DE\): пусть \(DE = 2\) см. Тогда по отношению подобия \(D_1E_1 : DE = \frac{3}{5}\), откуда \(D_1E_1 = DE \cdot \frac{3}{5} = 2 \cdot \frac{3}{5} = \frac{6}{5} = 1{,}2\) см. Таким образом, мы последовательно используем один и тот же коэффициент подобия \(\frac{3}{5}\) для перехода от большой фигуры к малой (умножаем на \(\frac{3}{5}\)) и обратно, от малой к большой (умножаем на \(\frac{5}{3}\)).

б) Так как фигуры \(ABCDE\) и \(A_1B_1C_1D_1E_1\) подобны, для любых соответствующих сторон выполняется одинаковое отношение. Поэтому можно записать несколько равных дробей: \(\frac{AB}{A_1B_1} = \frac{AE}{A_1E_1}\) (отношение соответствующих сторон через вершины \(A\) и \(E\)), а также \(\frac{AB}{BC} = \frac{A_1B_1}{B_1C_1}\) (отношение смежных сторон в одной фигуре равно такому же отношению в другой). Аналогично для отрезков около вершины \(D\): \(\frac{DE}{CD} = \frac{D_1E_1}{C_1D_1}\). Все эти равенства отражают один и тот же факт: отношение любых соответствующих сторон подобия постоянно и равно \(\frac{5}{3}\) (если считать большую фигуру к малой) или \(\frac{3}{5}\) (если малую к большой).

в) Перейдём к периметрам. Периметр многоугольника равен сумме его сторон. Для большой фигуры \(ABCDE\) по условию длины сторон равны \(3\) см, \(3\) см, \(4\) см, \(2\) см и \(2{,}5\) см. Тогда \(P_{ABCDE} = 3 + 3 + 4 + 2 + 2{,}5 = 14{,}5\) см. Для меньшей фигуры \(A_1B_1C_1D_1E_1\) стороны равны \(1{,}8\) см, \(1{,}8\) см, \(2{,}4\) см, \(1{,}2\) см и \(1{,}5\) см, значит \(P_{A_1B_1C_1D_1E_1} = 1{,}8 + 1{,}8 + 2{,}4 + 1{,}2 + 1{,}5 = 8{,}7\) см. Составляем отношение периметров: \(P_{ABCDE} : P_{A_1B_1C_1D_1E_1} = 14{,}5 : 8{,}7\). Чтобы выразить его дробью, запишем \(\frac{14{,}5}{8{,}7}\). Умножаем числитель и знаменатель на \(10\), получаем \(\frac{145}{87}\). Сокращаем дробь, деля числитель и знаменатель на \(29\): \(\frac{145}{87} = \frac{5}{3}\). Это отношение периметров совпадает с отношением соответствующих сторон большой и малой фигур, то есть \(P_{ABCDE} : P_{A_1B_1C_1D_1E_1} = \frac{5}{3}\).