ГДЗ по Алгебре 7 Класс Номер 12 Дорофеев, Суворова — Подробные Ответы

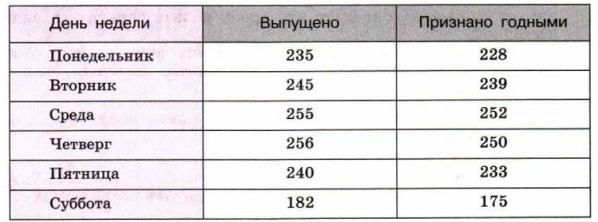
\(\frac{228}{235} \approx 0.9702\) – в понедельник

\(\frac{239}{245} \approx 0.9755\) – во вторник

\(\frac{252}{255} \approx 0.9882\) – в среду

\(\frac{250}{256} \approx 0.9766\) – в четверг

\(\frac{233}{240} \approx 0.9708\) – в пятницу

\(\frac{175}{182} \approx 0.9615\) – в субботу

Ответ: лучше всего завод работал в среду, хуже всего – в субботу.

\(\frac{228}{235} \approx 0.9702\) – в понедельник

\(\frac{239}{245} \approx 0.9755\) – во вторник

\(\frac{252}{255} \approx 0.9882\) – в среду

\(\frac{250}{256} \approx 0.9766\) – в четверг

\(\frac{233}{240} \approx 0.9708\) – в пятницу

\(\frac{175}{182} \approx 0.9615\) – в субботу

Задача требует определить, в какой день недели завод работал наиболее эффективно, а в какой — наименее. Эффективность работы завода за каждый день представлена в виде дроби, где числитель, вероятно, отражает количество произведенной годной продукции, а знаменатель — общее количество запланированной или произведенной продукции. Таким образом, отношение \(\frac{\text{Числитель}}{\text{Знаменатель}}\) представляет собой коэффициент эффективности, который всегда меньше единицы. Чем ближе этот коэффициент к единице, тем выше была производительность и качество работы. Для сравнения эффективности необходимо сравнить шесть полученных десятичных значений, соответствующих каждому дню недели.

Проанализируем и сравним полученные коэффициенты эффективности. В понедельник коэффициент составил приблизительно \(0.9702\), во вторник — \(0.9755\), в среду — \(0.9882\), в четверг — \(0.9766\), в пятницу — \(0.9708\), и в субботу — \(0.9615\). Для выявления лучшего дня необходимо найти максимальное значение среди этих шести чисел, а для худшего — минимальное. Сравнивая целые части и первые знаки после запятой (все равны \(0.9\)), переходим к сравнению последующих разрядов. Наибольшее значение, \(0.9882\), принадлежит среде. Это число выше всех остальных, что подтверждает максимальную эффективность работы завода в этот день. Минимальное значение, \(0.9615\), принадлежит субботе. Это число является наименьшим, что указывает на самую низкую эффективность за неделю.

Для более точной детализации сравнения можно рассмотреть значения с большей точностью. Например, для понедельника \(\frac{228}{235} \approx 0.97021\), для пятницы \(\frac{233}{240} \approx 0.97083\), что показывает, что пятница была немного эффективнее понедельника. Однако это не меняет общего вывода: максимальное значение \(\frac{252}{255} \approx 0.98823\) остается за средой, а минимальное \(\frac{175}{182} \approx 0.96153\) — за субботой. Таким образом, на основе сравнения коэффициентов, полученных как результат деления фактического показателя на плановый или общий, можно однозначно заключить о днях с наилучшей и наихудшей производительностью.

Ответ: лучше всего завод работал в среду, хуже всего – в субботу.