
Учебник «Алгебра. 7 класс» авторов Дорофеев Г.В. и Суворова С.Б. — это современное пособие, которое помогает школьникам сделать первые серьезные шаги в изучении алгебры. Книга рассчитана на широкий круг учеников и отличается продуманной структурой, доступным языком и большим количеством разнообразных задач.
ГДЗ по Алгебра 7 Класс Это надо знать Глава 5 Дорофеев, Суворова — Подробные Ответы
1. Назовите известные вам числовые промежутки и приведите соответ ствующие примеры.
2. На координатной прямой даны точки \(A(14)\), \(B(-6)\), \(C(a)\). На каком расстоянии от точки 0 находится каждая из этих точек?
3. Запишите формулу расстояния между точками координатной пря мой. По этой формуле найдите расстояние между точками \(A(-10,4)\) и \(B(2,3)\).
4. Каким равенством задаётся биссектриса I и III координатных углов?
5. Каким равенством задаётся биссектриса II и IV координатных углов?
6. Как называется график зависимости \(y = x^2\)? Укажите координаты нескольких точек, принадлежащих этому графику. Постройте этот график и опишите его свойства.
7. Изобразите на координатной плоскости график зависимости \(y = x^3\).
8. Изобразите на координатной плоскости график зависимости \(y = |x|\).
1. Числовые промежутки:
— открытый луч \( (x > 3; \; x < -5) \);
— замкнутый луч \( (x \geq 3; \; x \leq -5) \);
— интервал \((-1 < x < 5)\);
— отрезок \((-1 \leq x \leq 10)\);
— полуинтервал \((-5 < x \leq 3; \; -2 \leq x < 7{,}5)\).
2. Расстояние от точки 0:
\(A(14)\): \(|14 — 0| = |14| = 14\) единиц.
\(B(-6)\): \(|0 — (-6)| = |6| = 6\) единиц.
\(C(a)\): \(|a — 0| = |a| = a\) единиц.
3. Формула расстояния между точками: \(|b — a|\).
Для \(A(-10,4)\) и \(B(2,3)\):
\(AB = |2,3 — (-10,4)| = |12,7| = 12,7\) единиц.
4. Биссектриса I и III координатных углов задаётся равенством:
\(y = x\).
5. Биссектриса II и IV координатных углов задаётся равенством:
\(y = -x\).
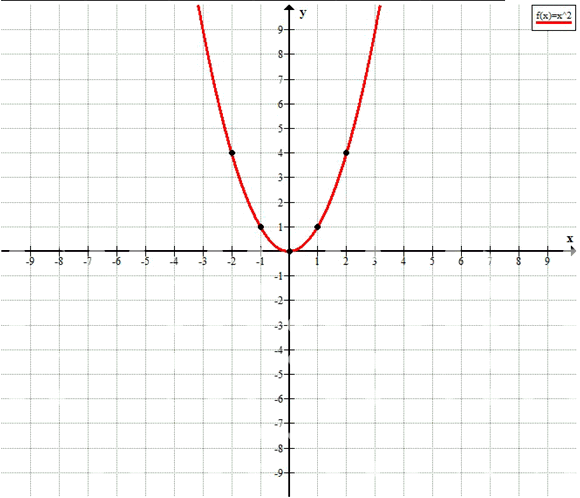
6. График \(y = x^2\) — парабола.
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | 4 | 1 | 0 | 1 | 4 |
Область определения: \((-\infty; +\infty)\).
Область значений: \(y \geq 0\).
При \(x=0\), \(y=0\).
Функция возрастает при \(x > 0\), убывает при \(x < 0\).
Минимум: \(y_{\text{наим}} = 0\), максимума нет.
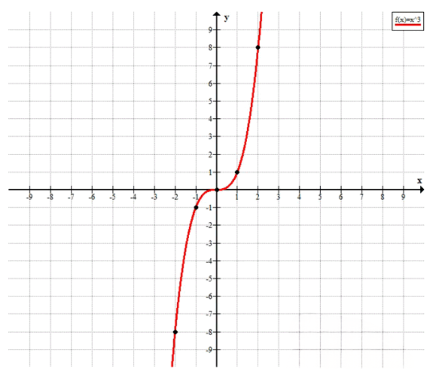
7. График \(y = x^3\).
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | -8 | -1 | 0 | 1 | 8 |
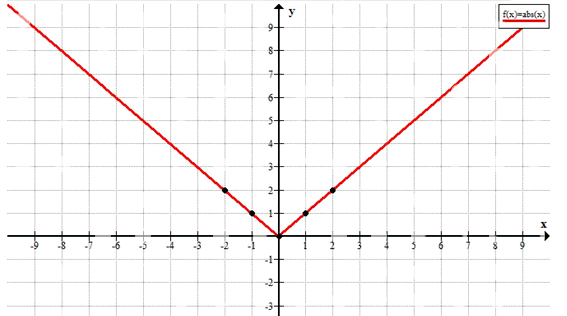
8. График \(y = |x|\).
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | 2 | 1 | 0 | 1 | 2 |
1. Числовые промежутки — это множества чисел, расположенных на числовой оси, которые описываются с помощью неравенств. Открытый луч — это множество всех чисел, больших некоторого числа, но не включающих это число, например, \(x > 3\), или меньших, чем другое число, например, \(x < -5\). В этом случае числа 3 и -5 не входят в множество. Замкнутый луч отличается тем, что включает в себя границы, то есть \(x \geq 3\) и \(x \leq -5\). Интервал — это множество чисел между двумя значениями, но без включения этих значений, например, \(-1 < x < 5\). Отрезок — это множество чисел между двумя значениями, включая эти значения, например, \(-1 \leq x \leq 10\). Полуинтервал — это промежуток, в котором одна граница включена, а другая нет, например, \(-5 < x \leq 3\) или \(-2 \leq x < 7{,}5\).
2. Расстояние от точки на числовой прямой до точки 0 определяется модулем разности координат. Для точки \(A(14)\) расстояние до 0 — это абсолютное значение числа 14, то есть \(|14 — 0| = |14| = 14\). Это значит, что точка находится на 14 единиц вправо от начала координат. Для точки \(B(-6)\) расстояние — это модуль числа \(-6\), то есть \(|0 — (-6)| = |6| = 6\), что означает 6 единиц влево от 0. Для точки \(C(a)\) расстояние до 0 — это \(|a — 0| = |a| = a\), где \(a\) — любое число, и расстояние всегда положительное или равно нулю.
3. Формула расстояния между двумя точками на координатной прямой — это модуль разности их координат: \(|b — a|\). Если взять точки \(A(-10,4)\) и \(B(2,3)\), то расстояние между ними находится как \(|2,3 — (-10,4)| = |2,3 + 10,4| = |12,7| = 12,7\) единиц. Это означает, что если представить эти точки на числовой оси, то расстояние между ними равно 12,7 единиц, что показывает, насколько они удалены друг от друга.
4. Биссектриса — это прямая, которая делит угол на две равные части. В координатной плоскости биссектриса I и III координатных углов задаётся уравнением \(y = x\). Это означает, что для любой точки на этой прямой координаты \(x\) и \(y\) равны, и прямая проходит через начало координат под углом 45 градусов к оси \(x\).
5. Аналогично, биссектриса II и IV координатных углов задаётся уравнением \(y = -x\). Здесь координаты \(y\) и \(x\) противоположны по знаку, и прямая также проходит через начало координат, но под углом -45 градусов к оси \(x\), разделяя второй и четвёртый квадранты.
6. График функции \(y = x^2\) называется параболой. Это кривая, симметричная относительно оси \(y\), которая открывается вверх. Рассмотрим несколько значений: при \(x = -2\), \(y = (-2)^2 = 4\); при \(x = -1\), \(y = 1\); при \(x = 0\), \(y = 0\); при \(x = 1\), \(y = 1\); при \(x = 2\), \(y = 4\). Таким образом, точки \((-2,4)\), \((-1,1)\), \((0,0)\), \((1,1)\), \((2,4)\) лежат на графике. Область определения функции — все действительные числа \((-\infty; +\infty)\), а область значений — все неотрицательные числа \(y \geq 0\), так как квадрат любого числа неотрицателен. При \(x=0\) функция достигает минимального значения \(y=0\). Функция возрастает при \(x > 0\) и убывает при \(x < 0\). Максимального значения функция не имеет.
7. График функции \(y = x^3\) — это кубическая парабола, которая проходит через начало координат и симметрична относительно начала координат. Рассмотрим значения: при \(x = -2\), \(y = (-2)^3 = -8\); при \(x = -1\), \(y = -1\); при \(x = 0\), \(y = 0\); при \(x = 1\), \(y = 1\); при \(x = 2\), \(y = 8\). Точки \((-2,-8)\), \((-1,-1)\), \((0,0)\), \((1,1)\), \((2,8)\) лежат на графике. Функция возрастает на всей области определения.
8. График функции \(y = |x|\) — это «V»-образная фигура, которая симметрична относительно оси \(y\). Значения функции равны абсолютному значению \(x\). При \(x = -2\), \(y = 2\); при \(x = -1\), \(y = 1\); при \(x = 0\), \(y = 0\); при \(x = 1\), \(y = 1\); при \(x = 2\), \(y = 2\). Точки \((-2,2)\), \((-1,1)\), \((0,0)\), \((1,1)\), \((2,2)\) лежат на графике. Область определения — все действительные числа, область значений — \(y \geq 0\). График состоит из двух лучей, один из которых направлен вверх вправо, другой — вверх влево.




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!