ГДЗ по Алгебра 7 Класс Это надо уметь Глава 5 Дорофеев, Суворова — Подробные Ответы

1. Изобразите на координатной прямой промежуток:
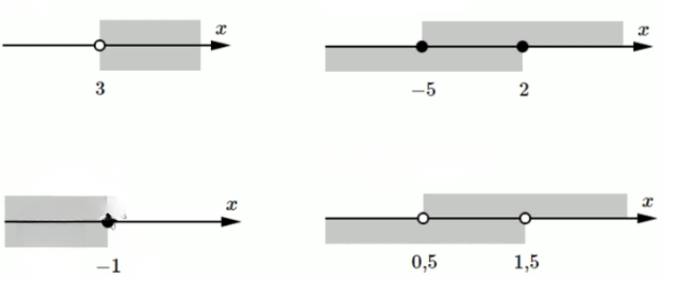
а) \( x > 3 \); б) \( x \leq -1 \); в) \(-5 < x < 2\); г) \(0,5 < x < 1,5\).

2. Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют условию:
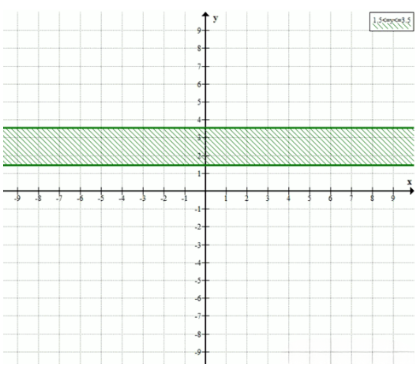
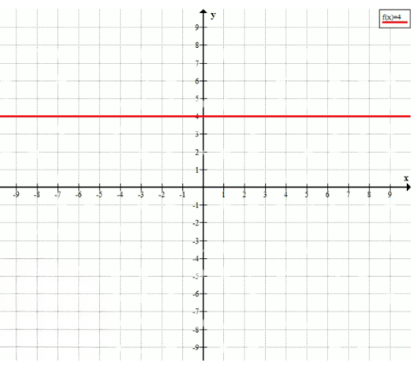
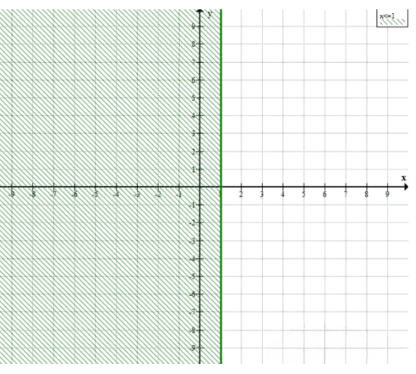
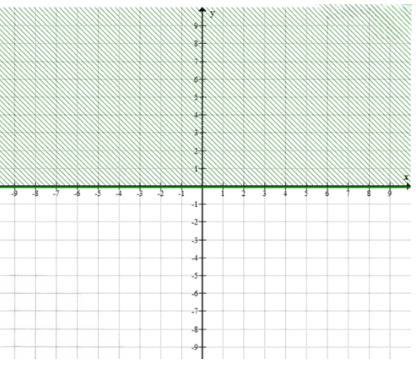
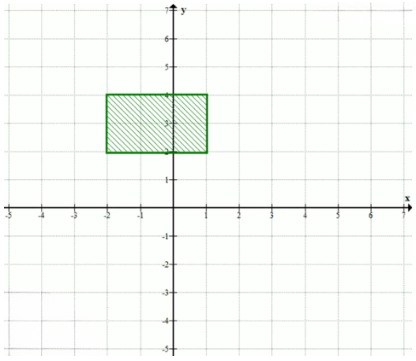
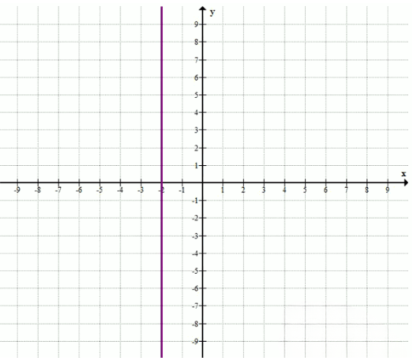
а) \( x = -2 \); б) \( y = 4 \); в) \( x \leq 1 \); г) \( y \geq 0 \); д) \( 1,5 \leq y \leq 3,5 \); е) \(-2 \leq x \leq 1\) и \(2 \leq y \leq 4\).

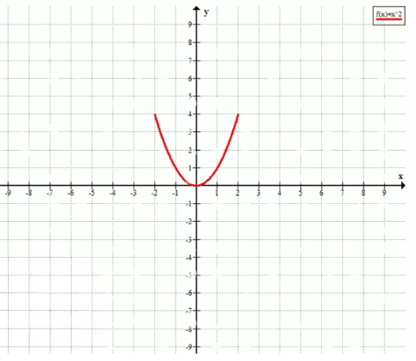
3. Изобразите на координатной плоскости множество точек, удовлетворяющих условиям \( y = x^2 \) и \(-2 \leq x \leq 2 \).

4. Постройте график зависимости:
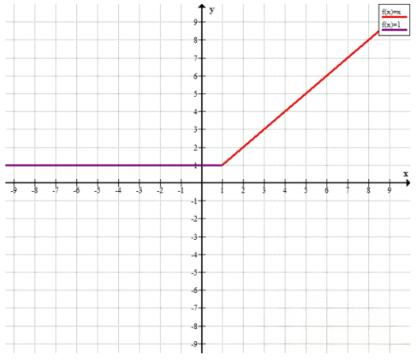
а) \( y = \begin{cases} x, & \text{при } x \geq 1 \\ 1, & \text{при } x < 1 \end{cases} \)
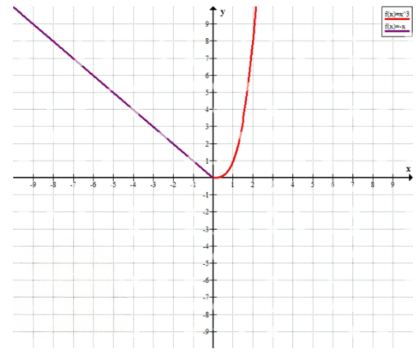
б) \( y = \begin{cases} x^3, & \text{при } x \geq 0 \\ -x, & \text{при } x < 0 \end{cases} \)

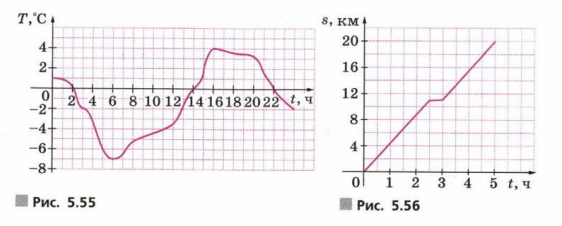
5. На рисунке 5.55 изображён график температуры воздуха 1 апреля 2010 г. в городе \( N \).
а) В какое время суток температура была равна 0°?
б) Когда в течение суток температура была положительной?
в) Какова была максимальная температура в этот день?

6. На рисунке 5.56 изображён график движения туриста от турлагеря до станции. Используя график, ответьте на следующие вопросы:
а) Сколько километров прошёл турист за первые 2 часа?
б) За сколько часов турист прошёл 15 км?
в) Сколько времени турист отдыхал?
г) Сколько всего километров прошёл турист?
д) Сколько всего часов шёл турист?

1. а) \( x > 3 \) — все числа больше 3, 3 не включается, значит точка 3 открытая, стрелка вправо.

б) \( x \leq -1 \) — все числа меньше или равны -1, точка -1 закрашена, стрелка влево.

в) \(-5 \leq x \leq 2\) — отрезок от -5 до 2 включительно, обе точки закрашены.

г) \(0{,}5 < x < 1{,}5\) — числа между 0,5 и 1,5, точки открытые, отрезок между ними.

2. а) \( x = -2 \) — вертикальная прямая через \( x = -2 \).

б) \( y = 4 \) — горизонтальная прямая через \( y = 4 \).

в) \( x \leq 1 \) — область слева от прямой \( x=1 \), включая её.

г) \( y \geq 0 \) — область выше оси \( x \), включая ось.

д) \( 1{,}5 \leq y \leq 3{,}5 \) — горизонтальная полоса между \( y=1{,}5 \) и \( y=3{,}5 \), включая границы.

е) \(-2 \leq x \leq 1\) и \(2 \leq y \leq 4\) — прямоугольник с углами \((-2, 2)\), \((-2, 4)\), \((1, 2)\), \((1, 4)\).

3. \( y = x^2 \), \( -2 \leq x \leq 2 \) — парабола на интервале от -2 до 2.

4. а) \( y = \begin{cases} x, & x \geq 1 \\ 1, & x < 1 \end{cases} \) — горизонтальная линия \( y=1 \) при \( x<1 \), прямая \( y=x \) при \( x \geq 1 \).

б) \( y = \begin{cases} x^3, & x \geq 0 \\ -x, & x < 0 \end{cases} \) — кубическая кривая при \( x \geq 0 \), прямая \( y=-x \) при \( x < 0 \).

5. а) Температура равна 0° в 2, 14 и 22 часа — точки пересечения с осью времени.

б) Температура положительная с 0 до 2 и с 14 до 22 часов — график выше оси времени.

в) Максимальная температура равна 4° С — наивысшая точка графика.

6. а) За первые 2 часа пройдено 9 км — скорость \( \frac{9}{2} = 4{,}5 \) км/ч.

б) За 4 часа пройдено 15 км — скорость \( \frac{15}{4} = 3{,}75 \) км/ч.

в) Отдых 30 минут — участок без изменения расстояния.

г) Всего пройдено 20 км — итоговое расстояние.

д) В пути 5 часов — общее время движения и отдыха.

1. а) Неравенство \( x > 3 \) означает, что рассматриваются все числа, которые строго больше числа 3. Это значит, что число 3 не включается в множество решений, а все числа, начиная с любого значения, чуть больше 3 и до бесконечности, входят в этот набор. На числовой оси точка, соответствующая числу 3, обозначается открытой точкой (или пустым кружком), чтобы показать, что это число не включено в множество. Затем от этой точки вправо проводится стрелка, указывающая на все числа больше 3.

б) Неравенство \( x \leq -1 \) охватывает все числа, которые меньше или равны числу -1. Здесь число -1 включено в множество, поэтому на числовой оси точка в позиции -1 обозначается закрашенной (сплошной) точкой. От этой точки влево проводится стрелка, показывающая, что включены все числа, меньшие -1, а также само число -1.

в) Двойное неравенство \(-5 \leq x \leq 2\) задаёт множество всех чисел от -5 до 2 включительно. Это значит, что и -5, и 2 входят в множество решений. На числовой оси обе эти точки отмечаются закрашенными точками, а между ними проводится отрезок, показывающий, что все числа между -5 и 2, включая границы, принадлежат множеству.

г) Неравенство \(0{,}5 < x < 1{,}5\) описывает все числа, которые строго больше 0,5, но строго меньше 1,5. Это значит, что сами числа 0,5 и 1,5 в множество не входят. На числовой оси точки 0,5 и 1,5 обозначаются открытыми точками, а между ними проводится отрезок или линия с открытыми концами, указывающая на все числа между этими значениями.

2. а) Уравнение \( x = -2 \) задаёт вертикальную прямую, которая проходит через точку на оси \( x \), где \( x = -2 \). Эта прямая параллельна оси \( y \), потому что значение \( x \) для всех точек на ней одинаково и равно -2, а \( y \) может принимать любые значения.

б) Уравнение \( y = 4 \) задаёт горизонтальную прямую, которая проходит через точку на оси \( y \), где \( y = 4 \). Эта прямая параллельна оси \( x \), так как для всех точек на ней значение \( y \) постоянно и равно 4, а \( x \) может быть любым.

в) Неравенство \( x \leq 1 \) задаёт область на плоскости, которая находится слева от вертикальной прямой \( x = 1 \), включая саму эту прямую. То есть все точки, у которых координата \( x \) меньше или равна 1, принадлежат этой области.

г) Неравенство \( y \geq 0 \) задаёт область на плоскости, которая находится выше оси \( x \) (где \( y = 0 \)), включая саму ось. Это значит, что все точки с неотрицательной координатой \( y \) входят в эту область.

д) Двойное неравенство \( 1{,}5 \leq y \leq 3{,}5 \) задаёт горизонтальную полосу на плоскости, ограниченную двумя параллельными прямыми \( y = 1{,}5 \) и \( y = 3{,}5 \), включая сами эти прямые. Все точки с координатой \( y \) между 1,5 и 3,5, включая границы, принадлежат этой полосе.

е) Система неравенств \(-2 \leq x \leq 1\) и \(2 \leq y \leq 4\) задаёт прямоугольную область на плоскости. Этот прямоугольник ограничен вертикальными линиями \( x = -2 \) и \( x = 1 \), а также горизонтальными линиями \( y = 2 \) и \( y = 4 \). Углы этого прямоугольника имеют координаты \((-2, 2)\), \((-2, 4)\), \((1, 2)\) и \((1, 4)\).

3. Функция \( y = x^2 \) представляет собой параболу, ветви которой направлены вверх. Ограничение \( -2 \leq x \leq 2 \) означает, что график строится только для значений \( x \) от -2 до 2 включительно. На интервале от -2 до 2 парабола имеет форму «чаши», при этом вершина параболы находится в начале координат \( (0, 0) \), а значения \( y \) растут по мере удаления от нуля в обе стороны. Это ограничение по \( x \) задаёт конечный участок параболы, а не всю бесконечную кривую.

4. а) Функция задана кусочно: \( y = \begin{cases} x, & x \geq 1 \\ 1, & x < 1 \end{cases} \). Для всех \( x \), меньших 1, значение функции постоянно и равно 1, то есть график на этом участке представляет собой горизонтальную прямую \( y = 1 \). При \( x \geq 1 \) функция равна \( y = x \), то есть график — это прямая с углом наклона 45°, проходящая через точку \( (1, 1) \). В точке \( x=1 \) происходит переход от константы к линейной функции, график непрерывен, так как при \( x=1 \) обе части совпадают по значению.

б) Функция задана кусочно: \( y = \begin{cases} x^3, & x \geq 0 \\ -x, & x < 0 \end{cases} \). Для \( x \geq 0 \) график — кубическая кривая, которая проходит через начало координат и растёт с увеличением \( x \). Для \( x < 0 \) функция равна \( y = -x \), что даёт прямую с отрицательным наклоном, проходящую через начало координат. В точке \( x=0 \) обе части функции равны нулю, график непрерывен, но меняется характер кривизны.

5. а) Температура равна 0° в три момента времени: в 2 часа, в 14 часов и в 22 часа. Это значит, что в эти часы температура достигала точки замерзания воды, и график температуры пересекал ось времени именно в этих точках. Эти моменты могут служить ориентирами для анализа изменения температуры в течение суток.

б) Температура была положительной в двух интервалах времени: с 0 до 2 часов и с 14 до 22 часов. Это означает, что в эти периоды температура была выше 0°, то есть тепло. График температуры на этих отрезках находится выше оси времени, что указывает на положительные значения температуры.

в) Максимальная температура в этот день достигала 4° С. Это значение является наивысшей точкой на графике температуры за весь день. Зная максимальную температуру, можно оценить климатические условия и характер погоды в этот период.

6. а) За первые 2 часа турист прошёл 9 км. Это можно определить по графику расстояния во времени, где за первые два часа путь увеличился на 9 километров. Средняя скорость на этом участке равна \( \frac{9}{2} = 4{,}5 \) км/ч.

б) За 4 часа турист прошёл 15 км. Это означает, что к моменту 4 часов суммарное пройденное расстояние составило 15 километров. Средняя скорость за первые 4 часа равна \( \frac{15}{4} = 3{,}75 \) км/ч, что меньше скорости первых двух часов, возможно из-за отдыха или замедления.

в) Турист отдыхал 30 минут. Это видно по участку графика, где расстояние не меняется при изменении времени, то есть турист не двигался. Длительность этого участка по времени составляет полчаса.

г) Всего турист прошёл 20 км. Итоговое расстояние, которое турист преодолел за всё время движения, равно 20 километрам. Это сумма всех пройденных за разные промежутки времени отрезков пути.

д) В пути турист был 5 часов. Общее время, в течение которого турист находился в движении и отдыхе, составляет 5 часов. Это время включает и периоды ходьбы, и период отдыха.